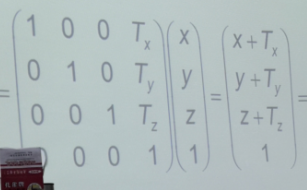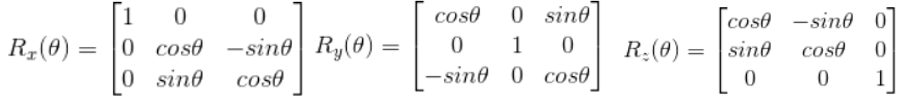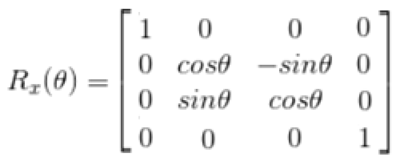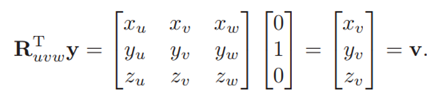如果觉得这篇太长,可到以下各单独blog数字化方法基础(一)_基础操作与生成四面体(Chapter 1-3) 数字化方法基础(二)_点的投影(Chapter 4-5) 数字化方法基础(三)_导入本地模型(Chapter 6) 数字化方法基础(四)_矩阵操作(Chapter 7)
ps.常用函数请看这里
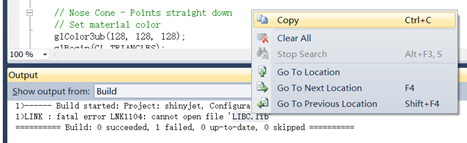
最近一次的代码(全)百度网盘: https://pan.baidu.com/s/1cmQwrqrWzPwYdklb7snTkg
Chapter1 VisualStudio2010 Express如何创建新工程
1、新建一个win32 Console Application工程,选择建立一个空项目(带预编译头的也可以,只不过大多数人不太习惯)
Chapter2 SB-WinSRC的使用方法
1、解压压缩包,得到一个SB-WinSRC文件夹
Chapter3 用OpenGL生成四面体
已知3点求法向量
1、具体思路为先根据已知3点做差求出两个向量,利用两个向量叉乘运算求出法向量,实现过程中尽量避免将所有代码集中到一个函数中,因为后续的操作(如投影点的计算)还需用到求法向量的函数,到时可直接调用。
1 2 3 4 5 void getvector (float a[3 ],float b[3 ],float vec[3 ]) { for (int i = 0 ;i < 3 ;i++) vec[i] = a[i] - b[i]; }
3、调用两次上述函数即可获得两个向量,接下来要做的就是拿这两个向量进行叉乘,以得到法向量
1 2 3 4 5 6 7 void crossproject (float vec1[3 ],float vec2[3 ],float n[3 ]) { n[0 ] = vec1[1 ]*vec2[2 ]-vec1[2 ]*vec2[1 ]; n[1 ] = vec1[2 ]*vec2[0 ]-vec1[0 ]*vec2[2 ]; n[2 ] = vec1[0 ]*vec2[1 ]-vec1[1 ]*vec2[0 ]; }
4、将上面两个函数简单封装一下如下
1 2 3 4 5 6 7 8 void project (float point1[3 ],float b[3 ],float c[3 ],float n[3 ]) { float vec1[3 ],vec2[3 ]; getvector(a,b,vec1); getvector(b,c,vec2); crossproject(vec1,vec2,n); }
5、这样一个求法向量的函数就写好了,使用方法如下例
1 2 3 4 5 6 double a[3 ] = {1.0 ,0.0 ,0.0 };double b[3 ] = {0.0 ,1.0 ,0.0 };double c[3 ] = {0.0 ,0.0 ,0.0 };double n[3 ];project(a,b,c,n);
生成四面体
1、使用OpenGL生成四面体的基本方法为,给定三个点和一个法向量 ,调用OpenDL的库函数,即可生成一个由这三点围成的三角形平面 ,四个三角形平面即可组成一个四面体 。
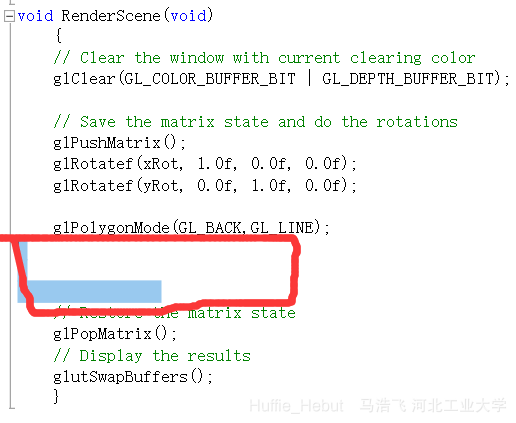
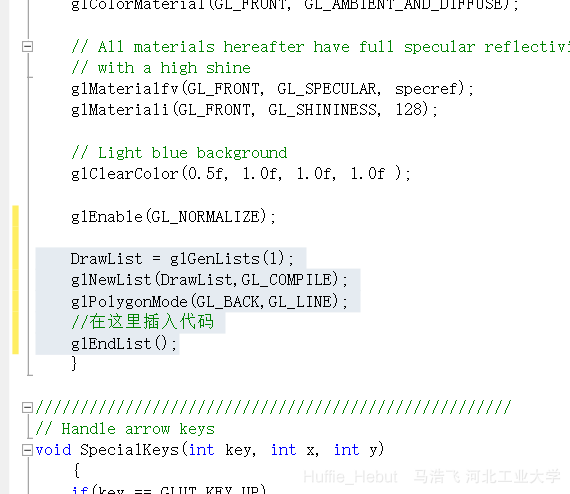
3、在RenderSenen()函数中的下图位置 写入glBegin()与glEnd()函数,并在二者之间插入画三角形的代码 。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 float rgfPoints4[12 ] = {-0.6f ,-0.6f ,-0.6f , 0.0f ,1.0f ,0.0f , 1.0f ,0.0f ,0.0f , 0.0f ,0.0f ,1.0f }; glColor3ub(255 ,255 ,0 ); glBegin(GL_TRIANGLES); DrawTriangle(rgfPoints4,rgfPoints4+3 ,rgfPoints4+6 ); DrawTriangle(rgfPoints4,rgfPoints4+9 ,rgfPoints4+3 ); DrawTriangle(rgfPoints4+3 ,rgfPoints4+9 ,rgfPoints4+6 ); DrawTriangle(rgfPoints4,rgfPoints4+6 ,rgfPoints4+9 ); glEnd();
4、在这里,glColor3ub、glBegin,glEnd均是OpenGL的库函数,不需要我们定义,直接调用即可,需要我们写的是DrawTriangle函数 ,接下来我们就开始定义DrawTriangle(),前面已经提到,需要用3个点和一个法向量 来确定一个平面,因此我们把第一节中生成法向量的函数复制到此文件的开头处,以便调用。
1 2 3 4 5 6 7 8 9 void DrawTriangle (float a[3 ],float b[3 ],float c[3 ]) { float n[3 ]; project(a,b,c,n); glNormal3fv(n); glVertex3fv(a); glVertex3fv(b); glVertex3fv(c); }
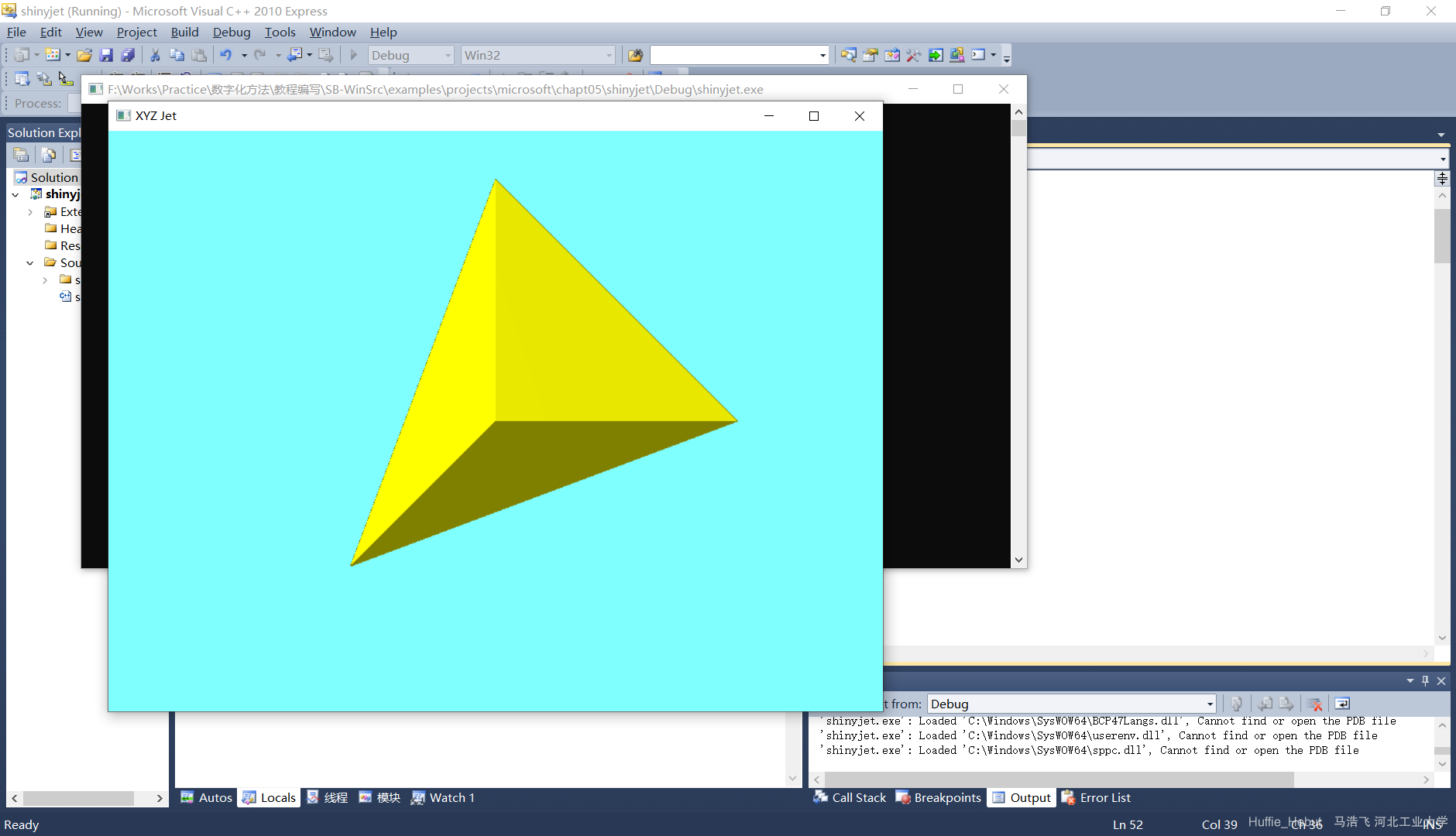
5、完成上述步骤后,进行调试,即可得到一个四面体
Chapter4 用OpenGL生成点的投影
计算点的投影的基本原理
如何编写程序实现点的投影
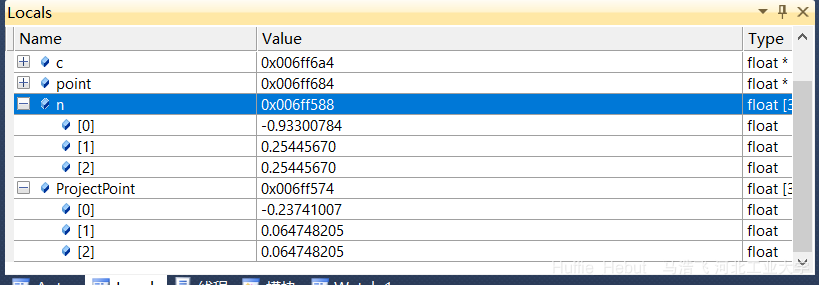
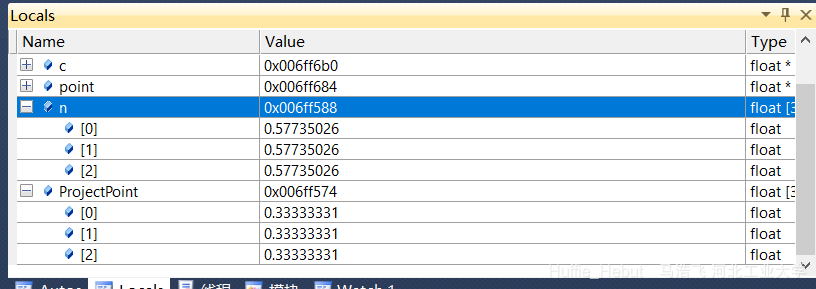
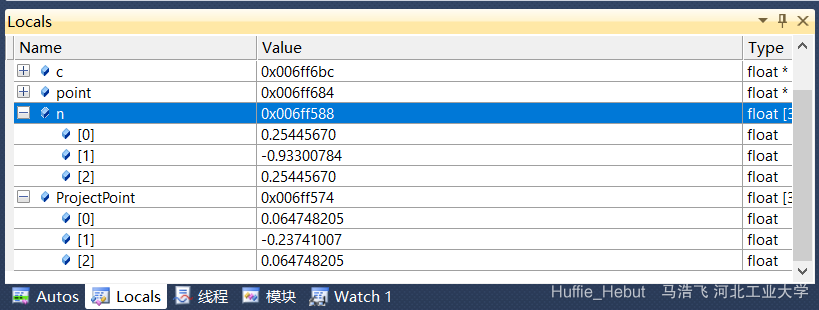
1、我们要实现点的投影就要知道投影点的坐标,由上一节可知,需要计算P0P1矢量 (这个直接调用上一讲求向量的函数),en向量 (需要写一个单位化函数),向量点乘 的函数
1 2 3 4 5 6 7 8 9 void Normalize (float n[3 ]) { float length; length = sqrt (n[0 ]*n[0 ]+n[1 ]*n[1 ]+n[2 ]*n[2 ]); for (int i = 0 ;i < 3 ;i++) n[i] /= length; }
3、进行向量点乘计算,并求N点坐标
1 2 3 4 5 6 7 8 9 10 11 12 13 void ProjectPointtoPoint (float point[3 ],float a[3 ],float n[3 ], float ProjectPoint[3 ]) { float vector_a_p[3 ]; float distance; for (int i = 0 ;i < 3 ;i++) vector_a_p[i] = point[i] - a[i]; distance = vector_a_p[0 ]*n[0 ]+vector_a_p[1 ]*n[1 ]+vector_a_p[2 ]*n[2 ]; for (int j = 0 ;j < 3 ;j++) ProjectPoint[j] = point[j] - n[j]*distance; }
4、经过上述步骤之后就获得投影点坐标,然后就可调用库函数显示投影点,以下为显示一个点的函数
1 2 3 4 5 6 7 8 9 10 11 12 13 14 void DrawPoint (float a[3 ],float b[3 ],float c[3 ],float point[3 ]) { float n[3 ]; project(a,b,c,n); Normalize(n); float ProjectPoint[3 ]; ProjectPointtoPoint(point,a,n,ProjectPoint); glVertex3fv(ProjectPoint); }
5、同三角形,在RenderSenen()函数中的画三角形的glEnd()后面 再次写入glBegin()与glEnd()函数,并在二者之间插入显示点的代码 。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 float point[3 ] = {0.0f ,0.0f ,0.0f };glColor3ub(0 ,0 ,0 ); glPointSize(6.0f ); glBegin(GL_POINTS); DrawPoint(rgfPoints4,rgfPoints4+3 ,rgfPoints4+6 ,point); DrawPoint(rgfPoints4,rgfPoints4+9 ,rgfPoints4+3 ,point); DrawPoint(rgfPoints4+3 ,rgfPoints4+9 ,rgfPoints4+6 ,point); DrawPoint(rgfPoints4,rgfPoints4+6 ,rgfPoints4+9 ,point); glEnd();
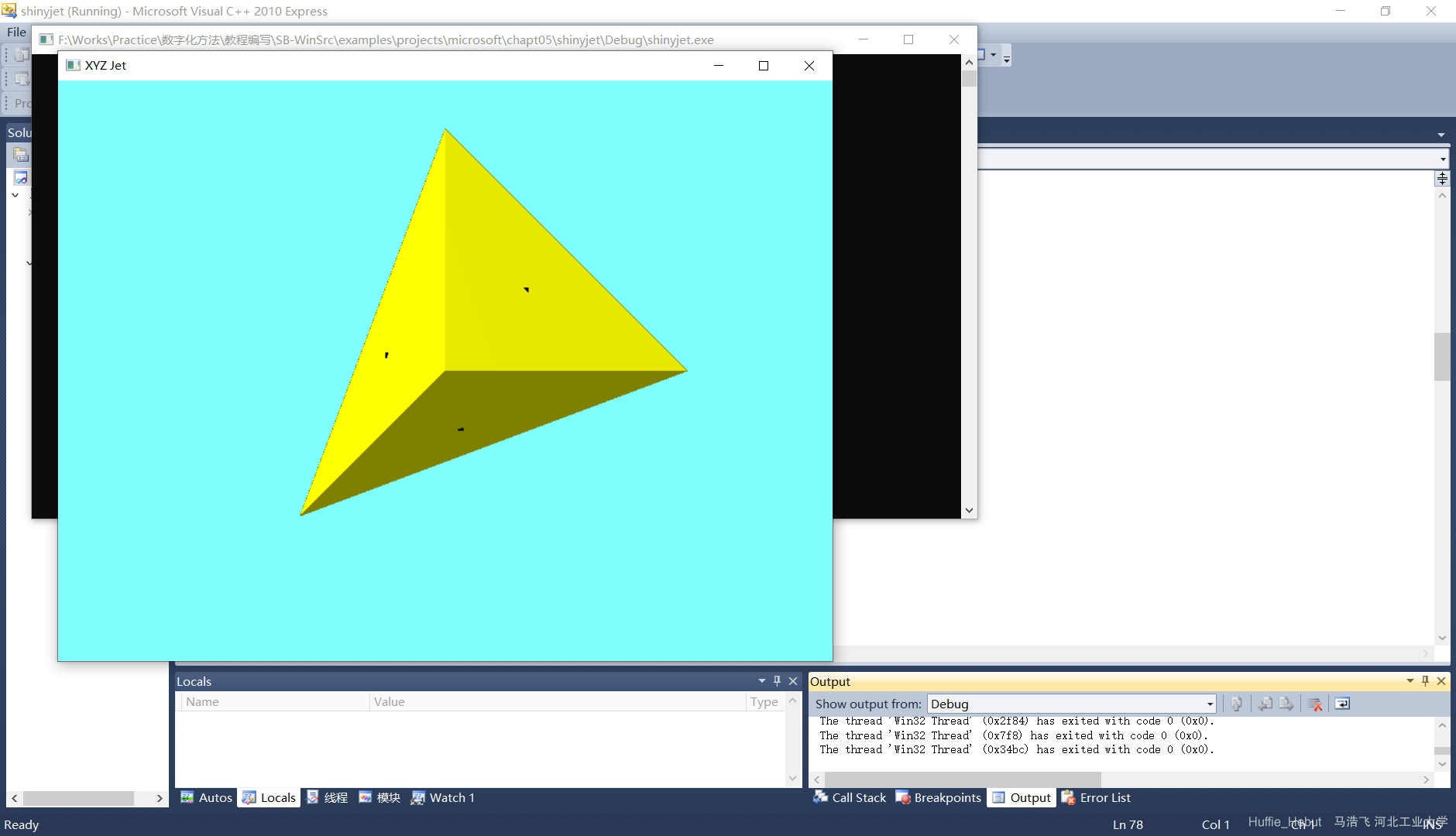
6、调试成功,显示如图
Chapter5 如何使用VS2010的调试功能
假如我写完程序调试后发现点没有显示,那么可以一步步调试,找出错误的地方。
Chapter 6 导入本地模型
图形的生成需要消耗一定的时间,简单的模型可能没有什么感觉,但是在模型十分复杂时,模型的生成就需要相当长的时间,这是我们不能忍受的。因此,将模型保存为本地文件,使用时直接加载进来,这就变得十分必要了,本节主要讲如何将创建一个列表以及如何加载一个列表。
如何创建一个列表
列表的基本原理就是将之前写的从glPolygonMode、glBegin开始,到glEnd 将这些代码用一行glCallList(DrawList)代替 ,其中DrawList内存放的就是之前生成四面体的代码了。glCallList就相当于把原来的四面体代码加载进来。定义一个GLuint类型的全局变量 (因为这个变量要在不同的函数使用,故须定义为全局变量)
2、将RenderScene函数(就是之前写glbegin和glEnd的地方)中的有关三角形的代码全部用glCallList函数代替
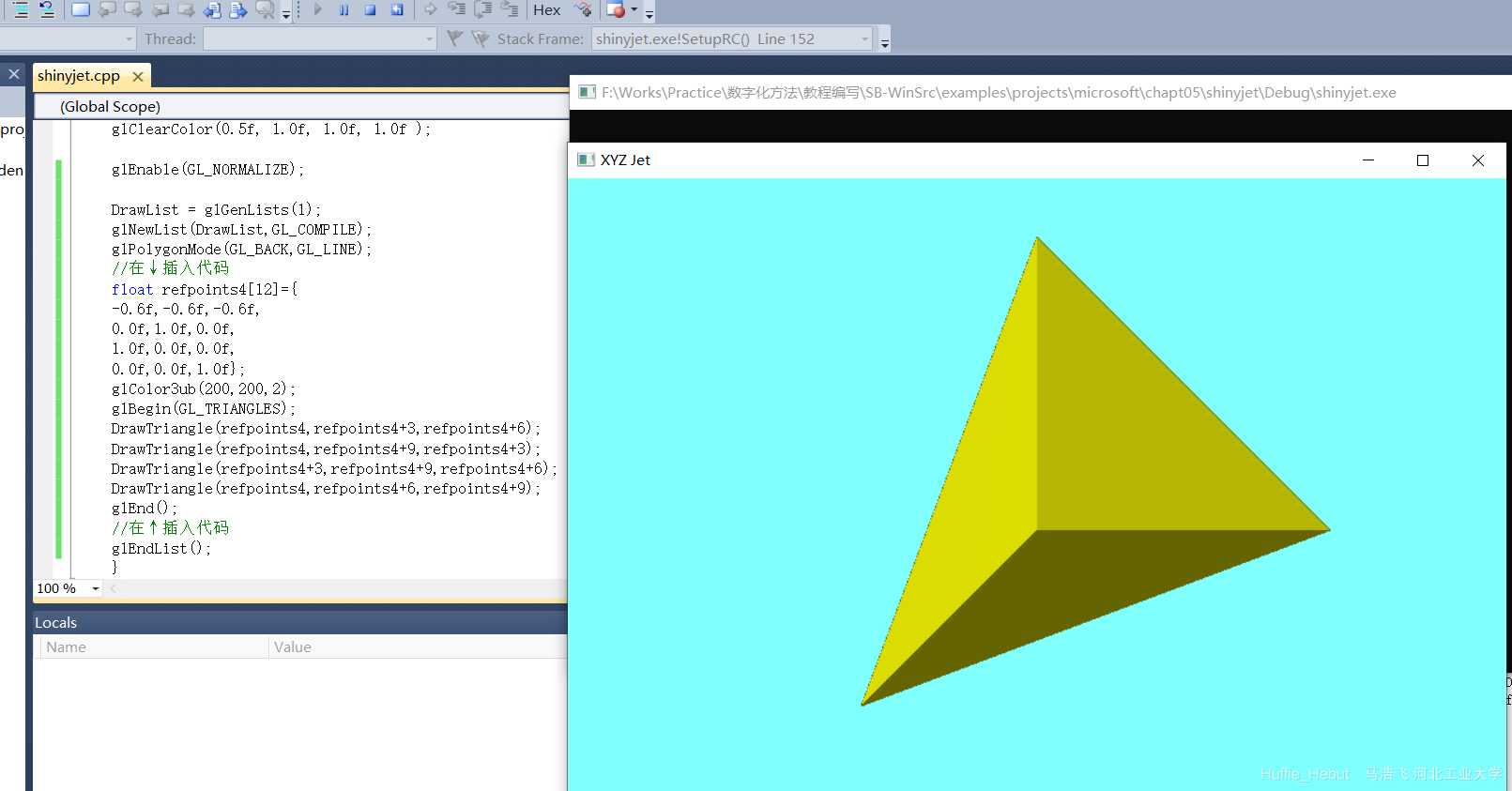
新建列表 ,框架 如下插入画四面体的代码 ,插入后结果如下图
如何读取本地模型
当我们需要读取本地文件中的模型时,如何操作呢
1 2 #include <fstream> using namespace std ;
2、在定义几个数组用来存放一会要读取的数据in >> String0指的是将读取到的字符存入String0中
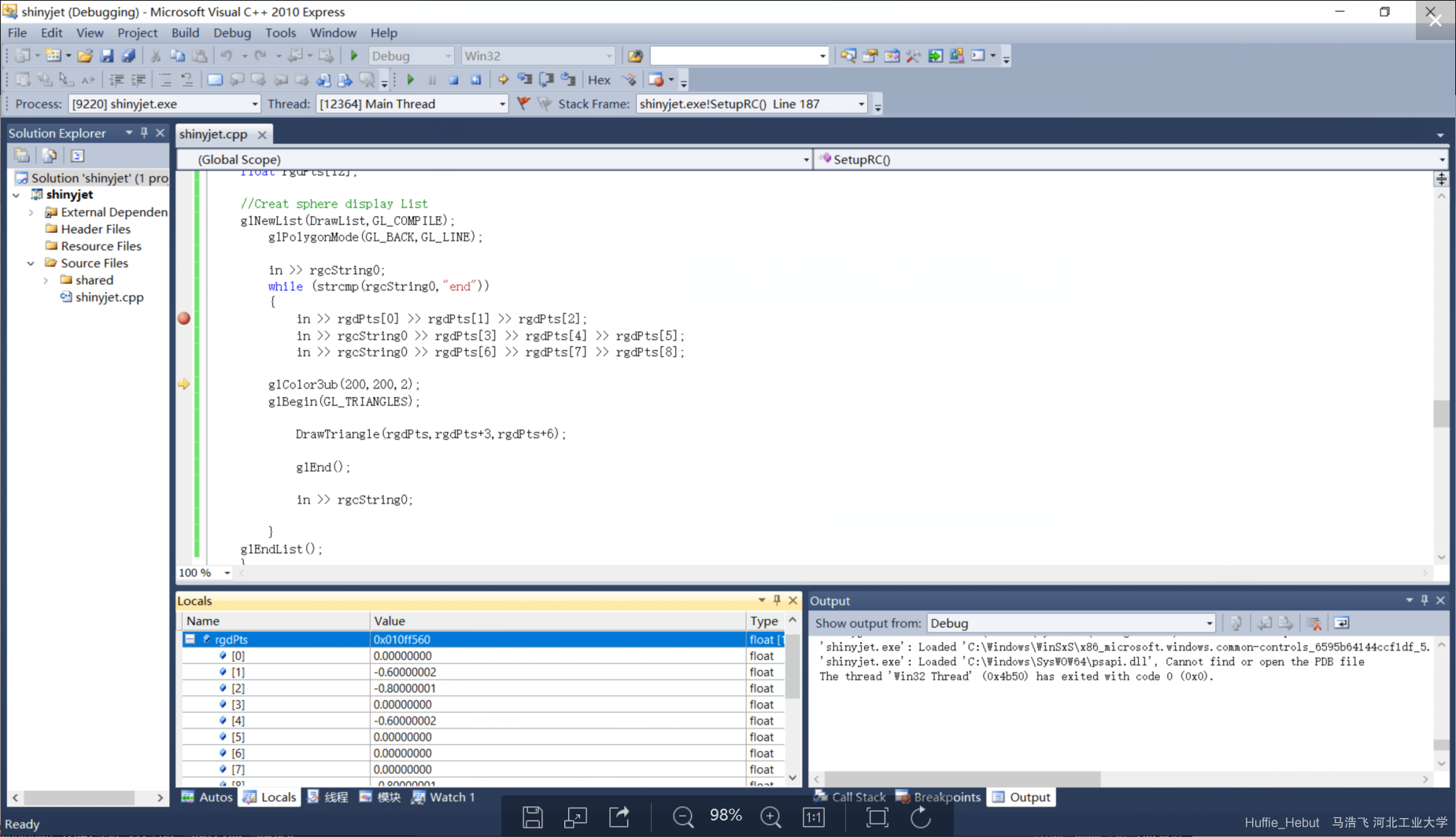
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 DrawList = glGenLists (1 ); glNewList (DrawList,GL_COMPILE); glPolygonMode (GL_BACK,GL_LINE); in >> String0 >> String0; while (strcmp (String0,"end" )) { in >> Points[0 ] >> Points[1 ] >> Points[2 ]; in >> String0 >> Points[3 ] >> Points[4 ] >> Points[5 ]; in >> String0 >> Points[6 ] >> Points[7 ] >> Points[8 ]; glColor3ub (200 ,200 ,2 ); glBegin (GL_TRIANGLES); DrawTriangle (Points,Points+3 ,Points+6 ); in >> String0; } glEndList ();
(因为用到了strcmp函数,需要引入头文件#include<string.h>)
无论是平面还是曲面,都是由无数个三角形组成的 ,只不过三角形数量无比多时,我们看起来它就是一个曲面,Part1.TXT文件中也是,每读取到三个点就画一个三角形,许许多多个三角形就会组成一个立体图形。每次循环结束 的时候都要保证String内存放 的是facet或者最后的endsolid 这个单词,以保证循环可以正常退出
1 2 3 4 5 6 7 8 9 void DrawTriangle (float a[3 ],float b[3 ],float c[3 ],float n[3 ]) glNormal3fv (n); glVertex3fv (a); glVertex3fv (b); glVertex3fv (c); }
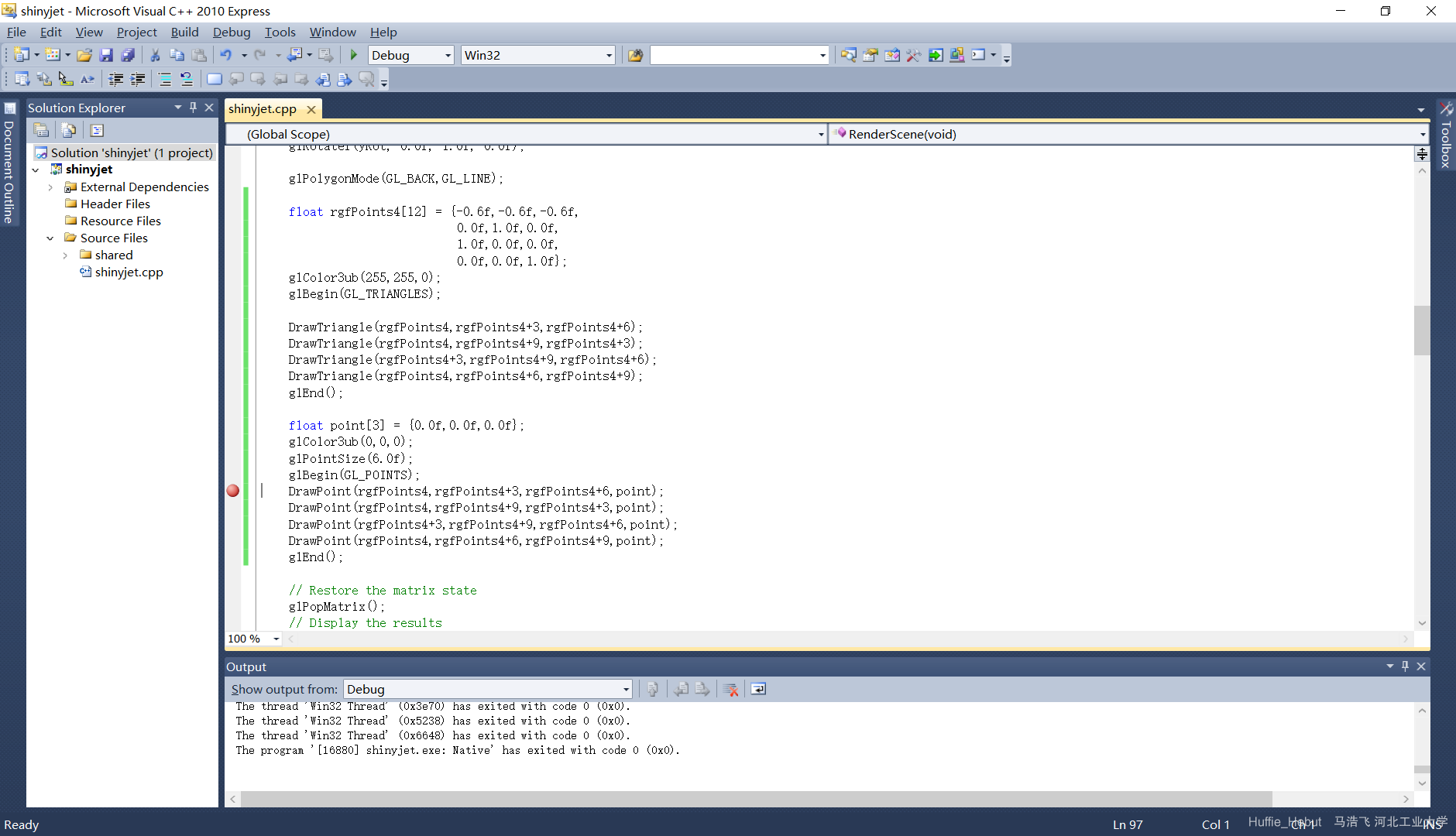
PS.如果程序出现错误,如何进行调试呢,首先在while循环里第一句前面设置断点,如下图
Chapter 7 矩阵操作
利用矩阵实现向量平移
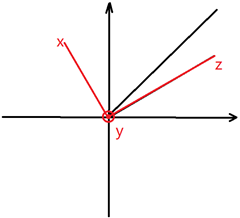
1、基本原理:如图,任意给定一个点的坐标(列向量)x,y,z。设置一个矩阵,利用矩阵的乘法运算即可将三个坐标进行平移
2、在了解了如何将一个列向量进行平移之后,我们就可以编写程序进行向量的平移操作了,我们打开生成螺旋线的程序,注意到螺旋线是由许许多多点组成的,下面这个for循环就是每次生成一个点,我们只需要吧每个点的坐标向量进行平移即可使整个螺旋线平移。
1. 获得一个点的坐标存入P0数组内
4、第一步,获得一个点的坐标存入P0数组内,这一步十分简单(注:除函数定义外,其余代码均在for循环内)float P0[3] = {x,y,z};
1 2 3 4 5 6 7 8 9 void Translate (float fx,float fy,float fz,float Translation[16 ]) { float I[16 ] = {1.0f ,0.0f ,0.0f ,0.0f ,0.0f ,1.0f ,0.0f ,0.0f ,0.0f ,0.0f ,1.0f ,0.0f ,0.0f ,0.0f ,0.0f ,1.0f }; I[12 ] = fx; I[13 ] = fy; I[14 ] = fz; for (int i = 0 ;i < 16 ;i++) Translation[i] = I[i]; }
这样操作之后就获得了如上面图片中的数组了。float P1[3];这十分简单,然后就是写一个矩阵乘法的运算,用Translation*P0,结果存入P1中。
1 2 3 4 5 void ApplyMatrix (float *P0,float *translation,float *P1) { for (int i = 0 ;i < 3 ;++i) P1[i] = P0[0 ]*translation[i]+P0[1 ]*translation[i+4 ]+P0[2 ]*translation[i+8 ]+translation[i+12 ]; }
7、有了设置操作矩阵的函数Translate,和矩阵相乘的函数ApplyMatrix,我们就可以平移点了。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 for (angle = 0.0f ; angle <= (2.0f *GL_PI)*3.0f ; angle += 0.1f ) { x = 50.0f *sin (angle); y = 50.0f *cos (angle); glVertex3f(x, y, z); float P0[3 ] = {x,y,z}; float P1[3 ]; float Translation[16 ]; Translate(0.0f ,30.0f ,0.0f ,Translation); ApplyMatrix(P0,Translation,P1); glVertex3f(P1[0 ], P1[1 ], P1[2 ]); z += 0.5f ; }
以上为螺旋线平移步骤
使用矩阵实现向量旋转
1、如何进行向量旋转由sin和cos组成的二阶方阵 ,就可以实现将向量(xa ya,)旋转为(xb,yb,) ,暂且叫做二阶的旋转操作矩阵三阶的旋转操作矩阵为以下三种 (分别为绕x,y,z轴旋转),大家带入检验一下即可知道,
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 for (angle = 0.0f ; angle <= (2.0f *GL_PI)*3.0f ; angle += 0.1f ) { x = 50.0f *sin (angle); y = 50.0f *cos (angle); glVertex3f(x, y, z); float P0[3 ] = {x,y,z}; float P1[3 ]; float Rotation[16 ] = {0 }; Rotate_x(-90 ,Rotation); ApplyMatrix(P0,multi,P1); glVertex3f(P1[0 ], P1[1 ], P1[2 ]); z += 0.5f ; }
因此,我们需要做的就是写一个函数 ,由参数(角度)生成一个旋转操作矩阵 ,这里需要注意的是,math.h头文件中有sin和cos的函数,直接sin(angle)即可调用,其中angle为弧度值,代码如下#define PI 3.14159)
1 2 3 4 5 6 7 8 9 10 11 12 void Rotate_x (float angle,float *rotation) { angle = angle/180.0 *PI; rotation[5 ] = cos (angle); rotation[6 ] = sin (angle); rotation[9 ] = -sin (angle); rotation[10 ] = cos (angle); rotation[0 ] = 1 ; rotation[15 ] = 1 ; }
这样我们得到了旋转操作矩阵,经“主函数”调用即可实现向量的旋转
如何让图形既平移又旋转
一个很简单的思路就是先后调用平移和旋转操作的函数 ,像下面这样
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 for (angle = 0.0f ; angle <= (2.0f *GL_PI)*3.0f ; angle += 0.1f ) { x = 50.0f *sin (angle); y = 50.0f *cos (angle); glVertex3f(x, y, z); float P0[3 ] = {x,y,z}; float P1[3 ]; float P2[3 ]; float Translation[16 ]; Translate(0.0f ,60.0f ,0.0f ,Translation); ApplyMatrix(P0,Translation,P1); float Rotation[16 ] = {0 }; Rotate_x(-90 ,Rotation); ApplyMatrix(P1,Rotation,P2); glVertex3f(P2[0 ], P2[1 ], P2[2 ]); z += 0.5f ; }
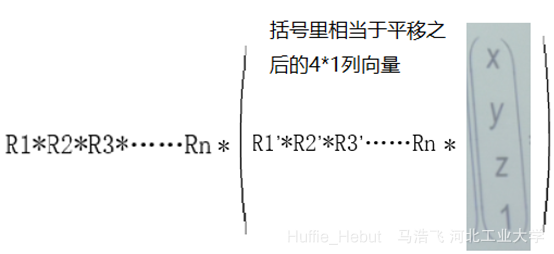
但是这显然不是我们想要的,我们想一步就完成平移操作,不需要中间P1的出现,那么就需要将平移操作矩阵和旋转操作矩阵相乘,得到的仍为一个四阶矩阵,再拿这个新的四阶矩阵左乘列向量xy,即可将列向量既平移又旋转 。如何理解? R2 R3*……Rn,T = R1’R2’R3’……Rn’ T 列向量 就代表把列向量平移又旋转
1 2 3 4 5 6 7 void mul (float *rotation,float *translation,float *tran) { for (int i = 0 ;i < 4 ;i++) for (int j = 0 ;j < 4 ;j++) for (int k = 0 ;k < 4 ;k++) tran[4 *i+j] += rotation[4 *k+j]*translation[4 *i+k]; }
注意这个是用16个元素的变量代表一个矩阵,下标表示比较麻烦,大家可以在纸上写一下
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 for (angle = 0.0f ; angle <= (2.0f *GL_PI)*3.0f ; angle += 0.1f ) { x = 50.0f *sin (angle); y = 50.0f *cos (angle); glVertex3f(x, y, z); float P0[3 ] = {x,y,z}; float P1[3 ]; float Translation[16 ]; Translate(0.0f ,60.0f ,0.0f ,Translation); float Rotation[16 ] = {0 }; Rotate_x(-90 ,Rotation); float multi[16 ] = {0 }; mul(Rotation,Translation,multi); ApplyMatrix(P0,multi,P1); glVertex3f(P1[0 ], P1[1 ], P1[2 ]); z += 0.5f ; }
以上即利用矩阵实现向量的平移与旋转操作
坐标系的旋转
1、目标 :2、基本概念 :三阶方阵左乘一个原坐标系的点 ,即可将这个点坐标旋转为新坐标系的对应坐标 3、如何生成Ruvw矩阵
1 2 3 4 5 6 7 8 9 10 11 12 13 14 void RotateCoor (float *z,float *Rotation) { Rotation[3 ] = 0 ; Rotation[15 ] = 1 ; Normalize(z); for (int i = 0 ;i < 3 ;i++) Rotation[8 +i] = z[i]; Rotation[4 ] = -z[1 ]; Rotation[5 ] = z[0 ]; Normalize(Rotation+4 ); crossproject(z,Rotation+4 ,Rotation); Normalize(Rotation); }
和之前平移与旋转一样 ,用这个矩阵×P0点 ,即可得到坐标轴旋转后的点P1
让图形显示在屏幕中心且绕中心转动
1.首先我们要知道,OpenGL生成的对话框的长和宽是可以设置的,我们需要让对话框的宽高比与我们要生成的图像的宽高比相同,并且对话框要比图像稍大一些。如果ModelHeight/h > ModelWidth/w,说明对话框比较高(模型比较宽),因此要尽可能满足模型的宽 ,比如让对话框的宽为模型宽的2.5倍 (让对话框稍大一些),则对话框的高就为 对话框的高/模型的高 * 模型的宽 。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 void ChangeSize (int w, int h) { GLfloat fAspect; GLfloat lightPos[] = { -50.f , 50.0f , 100.0f , 1.0f }; if (h == 0 ) h = 1 ; glViewport(0 , 0 , w, h); glMatrixMode(GL_PROJECTION); glLoadIdentity(); fAspect = (GLfloat) w / (GLfloat) h; float scale = 2.5 ; float ScaleHeight,ScaleWidth,ModelWidth,ModelHeight; ModelWidth = PointMax[0 ]-PointMin[0 ]; ModelHeight = PointMax[1 ]-PointMin[1 ]; if (w*ModelHeight > h*ModelWidth) { ScaleHeight = scale * ModelHeight; ScaleWidth = scale * ModelHeight * w / h; } else { ScaleWidth = scale * ModelWidth; ScaleHeight = scale * ModelWidth * h / w; } glOrtho(0.5 * (PointMax[0 ] - PointMin[0 ]) - 0.5 * ScaleWidth,0.5 * (PointMax[0 ] - PointMin[0 ]) + 0.5 * ScaleWidth,0.5 * (PointMax[1 ] - PointMin[1 ]) - 0.5 * ScaleWidth,0.5 * (PointMax[1 ] - PointMin[1 ]) + 0.5 * ScaleWidth,-2.0 ,2.0 ); glMatrixMode(GL_MODELVIEW); glLoadIdentity(); glLightfv(GL_LIGHT0,GL_POSITION,lightPos); }
4、如何编程找出模型上对角线的两个点
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 while (strcmp (String0,"endsolid" )) { in >> String0; in >> n[0 ] >> n[1 ] >> n[2 ]; in >> String0 >> String0 >> String0 >> Points[0 ] >> Points[1 ] >> Points[2 ]; in >> String0 >> Points[3 ] >> Points[4 ] >> Points[5 ]; in >> String0 >> Points[6 ] >> Points[7 ] >> Points[8 ]; for (float * point = Points + 3 ;point < Points + 11 ;point += 3 ) { for (int j = 0 ;j < 3 ;j++) { if (Points[j]<PointMin[j]) { PointMin[j] = Points[j]; } if (Points[j]>PointMax[j]) { PointMax[j] = Points[j]; } } } glColor3ub(255 ,255 ,0 ); glBegin(GL_TRIANGLES); DrawTriangle(Points,Points+3 ,Points+6 ,n); glEnd(); in >> String0 >> String0>> String0; } (注意,因为PointMin和PointMax既在SetupRC函数里使用又在Changesize函数里使用,故需要定义为全局变量,如下float PointMin[3 ] = {1.0e38 f,1.0e38 f,1.0e38 f};float PointMax[3 ] = {1.0e-38 f,1.0e-38 f,1.0e-38 f};)
5、现在看起来可以了,我们把对话框设置成了和模型等比例,对称中心重合,但还需要更改一个地方就是,我们生成的模型中心和我们旋转轴的中心不是重合的 ,我们如何实现按下键盘时,让模型绕原点转动,而不是绕其他轴运动。要让模型绕自己中心旋转,可以先把模型平移到坐标轴原点处(原点与模型中心重合),进行旋转,然后在平移回原来位置,这样看上去就是模型绕自己中心旋转了 ,具体代码如下:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 void RenderScene (void ) { glClear(GL_COLOR_BUFFER_BIT | GL_DEPTH_BUFFER_BIT); glPushMatrix(); float Translation[16 ]; Translate(0.5f * (PointMax[0 ] + PointMin[0 ]),0.5f * (PointMax[1 ] + PointMin[1 ]),0.5f * (PointMax[2 ] + PointMin[2 ]),Translation); glMultMatrixf(Translation); glRotatef(xRot,1.0f ,0.0f ,0.0f ); glRotatef(yRot,0.0f ,1.0f ,0.0f ); Translate(-0.5f * (PointMax[0 ] + PointMin[0 ]),-0.5f * (PointMax[1 ] + PointMin[1 ]),-0.5f * (PointMax[2 ] + PointMin[2 ]),Translation); glMultMatrixf(Translation); glCallList(DrawList); glPopMatrix(); glutSwapBuffers(); }
经过修改这三个地方就实现了让模型能够正常的显示在屏幕中心且绕模型自己的中心转动
Chapter 8 造小车
装配一个小车
组装小车开始了请先掌握装载泵体模型的相关操作 先新建一个列表DrawList ,然后将模型存入此列表中 ,最后在通过glCallList()函数召唤列表即可生成一个模型 。现在我们要做的就是同时生成许多个模型,那么如何同时生成许多模型呢,只要新建许多列表,然后把它们一个一个召唤出来(glCallList)就可以了 。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 void CreatGLList (char *filename,int R,int G,int B,GLuint *listname) { ifstream in (filename) ; if (!in) _ASSERT(0 ); char String0[30 ]; in >> String0 >> String0>> String0; *listname = glGenLists(1 ); float Points[12 ]; float n[3 ]; glNewList(*listname,GL_COMPILE); glPolygonMode(GL_BACK,GL_LINE); while (strcmp (String0,"endsolid" )) { in >> String0; in >> n[0 ] >> n[1 ] >> n[2 ]; in >> String0 >> String0 >> String0 >> Points[0 ] >> Points[1 ] >> Points[2 ]; in >> String0 >> Points[3 ] >> Points[4 ] >> Points[5 ]; in >> String0 >> Points[6 ] >> Points[7 ] >> Points[8 ]; for (float * point = Points + 3 ;point < Points + 11 ;point += 3 ) { for (int j = 0 ;j < 3 ;j++) { if (Points[j]<PointMin[j]) { PointMin[j] = Points[j]; } if (Points[j]>PointMax[j]) { PointMax[j] = Points[j]; } } } glColor3ub(R,G,B); glBegin(GL_TRIANGLES); DrawTriangle(Points,Points+3 ,Points+6 ); glEnd(); in >> String0 >> String0>> String0; } glEndList(); }
3.我们有了新建列表的函数之后,然后就可以加载文件了……吗?注意,在使用函数之前先在文件开头定义几个列表变量(GLuint类型变量) ,这个几个变量是用来存放各个模型的,没有这些变量就调用函数,软件会在参数上划红线,也就是它不知道把模型读取进来之后存到哪里去。新建六个模型列表就用六次这个函数就可以了 ,比直接复制一大段读取模型的文件简化了不少。就像下面这样
让小车动起来
本节的目的是让小车动起来!难度稍大,各位仔细听我娓娓道来函数用来读取按键 ,读取之后利用平移旋转之类的矩阵各个部分运动起来 。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 void keyboard (unsigned char key,int x,int y) { static float ShoveStep = 3.0f ; if (ShoveRot > 60.0f ) ShoveRot = -3.0f ; else if (ShoveRot < -60.0f ) ShoveRot = 3.0f ; switch (key) { case 'w' :ShoveRot+=ShoveStep;glutPostRedisplay();break ; case 's' :ShoveRot-=ShoveStep;glutPostRedisplay();break ; } static float MainLinkStep = 3.0f ; if (MainLinkRot > 60.0f ) MainLinkRot = -3.0f ; else if (MainLinkRot < -60.0f ) MainLinkRot = 3.0f ; switch (key) { case 'a' :MainLinkRot+=MainLinkStep;glutPostRedisplay();break ; case 'd' :MainLinkRot-=MainLinkStep;glutPostRedisplay();break ; } static float MainBodyStep = 3.0f ; if (MainBodyRot > 60.0f ) MainBodyRot = -3.0f ; else if (MainBodyRot < -60.0f ) MainBodyRot = 3.0f ; switch (key) { case 'j' :MainBodyRot+=MainBodyStep;glutPostRedisplay();break ; case 'k' :MainBodyRot-=MainBodyStep;glutPostRedisplay();break ; } static float GroundStep = 3.0f ; if (GroundRot > 60.0f ) GroundRot = -3.0f ; else if (GroundRot < -60.0f ) GroundRot = 3.0f ; switch (key) { case 'q' :GroundRot+=GroundStep;glutPostRedisplay();break ; case 'e' :GroundRot-=GroundStep;glutPostRedisplay();break ; } static float FrontWheelsStep = 3.0f ; if (FrontWheelsRot > 60.0f ) FrontWheelsRot = -3.0f ; else if (FrontWheelsRot < -60.0f ) FrontWheelsRot = 3.0f ; switch (key) { case 'z' :FrontWheelsRot+=FrontWheelsStep;glutPostRedisplay();break ; case 'x' :FrontWheelsRot-=FrontWheelsStep;glutPostRedisplay();break ; } static float BackWheelsStep = 3.0f ; if (BackWheelsRot > 60.0f ) BackWheelsRot = -3.0f ; else if (BackWheelsRot < -60.0f ) BackWheelsRot = 3.0f ; switch (key) { case 'c' :BackWheelsRot+=BackWheelsStep;glutPostRedisplay();break ; case 'v' :BackWheelsRot-=BackWheelsStep;glutPostRedisplay();break ; } }
这样我们就成功的读取到了按键并能够根据按键的不同,相应的角度变量发生改变(函数中的按键可以自己设置,根据个人喜好)glLoadIdentity();生成一个单位阵并设置为当前阵
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 void RenderScene (void ) { glClear(GL_COLOR_BUFFER_BIT | GL_DEPTH_BUFFER_BIT); glPushMatrix(); Translate(0.5f * (PointMax[0 ] + PointMin[0 ]),0.5f * (PointMax[1 ] + PointMin[1 ]),0.5f * (PointMax[2 ] + PointMin[2 ]),Translation); glMultMatrixf(Translation); glRotatef(xRot,1.0f ,0.0f ,10.0f ); glRotatef(yRot,0.0f ,1.0f ,0.0f ); Translate(-0.5f * (PointMax[0 ] + PointMin[0 ]),-0.5f * (PointMax[1 ] + PointMin[1 ]),-0.5f * (PointMax[2 ] + PointMin[2 ]),Translation); glMultMatrixf(Translation); glPushMatrix(); glCallList(MainBody); glPopMatrix(); glPushMatrix(); Translate(0 ,float (-4.89 /1000.0 ),float (-39.75 /1000.0 ),Translation); glMultMatrixf(Translation); Rotate_x(ShoveRot,Rotation); glMultMatrixf(Rotation); Translate(0 ,float (4.89 /1000.0 ),float (39.75 /1000.0 ),Translation); glMultMatrixf(Translation); glCallList(BackWheels); glLoadIdentity(); Translate(0.5f * (PointMax[0 ] + PointMin[0 ]),0.5f * (PointMax[1 ] + PointMin[1 ]),0.5f * (PointMax[2 ] + PointMin[2 ]),Translation); glMultMatrixf(Translation); glRotatef(xRot,1.0f ,0.0f ,10.0f ); glRotatef(yRot,0.0f ,1.0f ,0.0f ); Translate(-0.5f * (PointMax[0 ] + PointMin[0 ]),-0.5f * (PointMax[1 ] + PointMin[1 ]),-0.5f * (PointMax[2 ] + PointMin[2 ]),Translation); glMultMatrixf(Translation); glPushMatrix(); Translate(0 ,float (-6.63 /1000.0 ),float (16.50 /1000.0 ),Translation); glMultMatrixf(Translation); Rotate_x(ShoveRot,Rotation); glMultMatrixf(Rotation); Translate(0 ,float (6.63 /1000.0 ),float (-16.50 /1000.0 ),Translation); glMultMatrixf(Translation); glCallList(FrontWheels); glPopMatrix(); Translate(0 ,0 ,float (-10 /1000.0 ),Translation); glMultMatrixf(Translation); glRotatef(GroundRot,0.0f ,1.0f ,0.0f ); Translate(0 ,0 ,float (10 /1000.0 ),Translation); glMultMatrixf(Translation); glCallList(Ground); Translate(0 ,float (21.74 /1000 ),float (4.06 /1000.0 ),Translation); glMultMatrixf(Translation); Rotate_x(MainLinkRot,Rotation); glMultMatrixf(Rotation); Translate(0 ,float (-21.74 /1000 ),float (-4.06 /1000.0 ),Translation); glMultMatrixf(Translation); glCallList(MainLink); Translate(0 ,float (31.74 /1000.0 ),float (53.46 /1000.0 ),Translation); glMultMatrixf(Translation); Rotate_x(ShoveRot,Rotation); glMultMatrixf(Rotation); Translate(0 ,float (-31.74 /1000.0 ),float (-53.46 /1000.0 ),Translation); glMultMatrixf(Translation); glCallList(Shove); glPopMatrix(); glutSwapBuffers(); }
这些代码都可在博客开头的网盘里自行提取
Continue……