【深度学习笔记08】经典神经网络
LeNet-5
该网络的作用可用于手写数字识别。
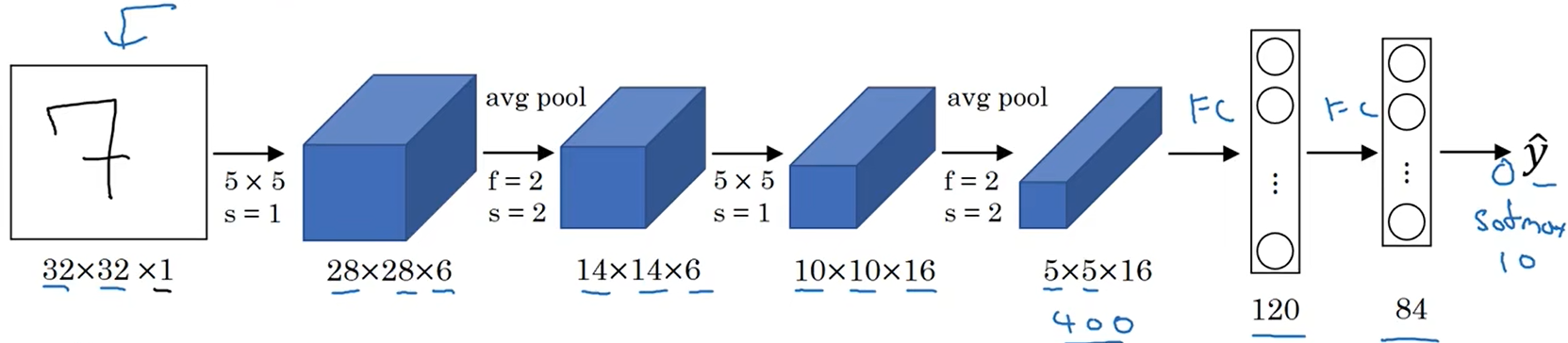
- 输入:32x32x1的手写数字图片
- 卷积:f=5, s=1, filters=6,图像变为28x28x6
- 平均池化:f=2, s=2,图像变为14x14x6
- 卷积:f=5, s=2, filters=16,图像变为10x10x16
- 平均池化:f=2, s=2,图像变为5x5x16
- 全连接层:400 -> 120
- 全连接层:120 -> 84
- 分类:10类输出
共计约6万个参数,使用sigmoid作为激活函数。
AlexNet
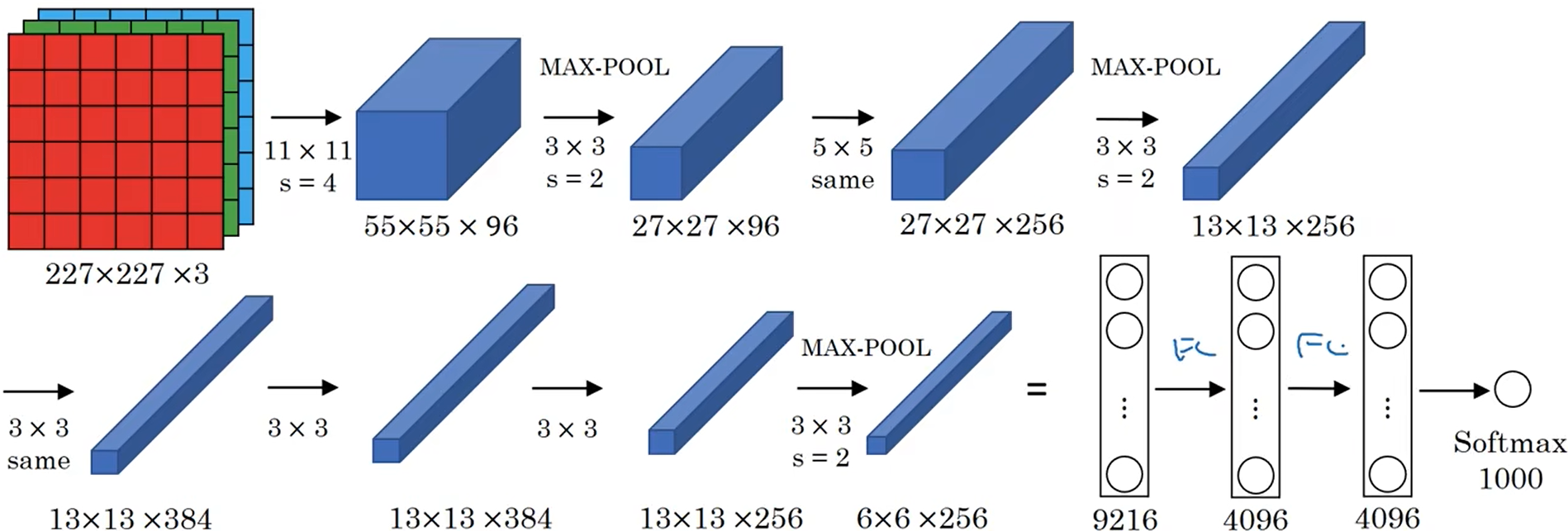
- 输入:227x227x3的包含目标物体的图片
- 卷积:f=11, s=4, filters=96,图像变为55x55x96
- 最大池化:f=3, s=2,图像变为27x27x96
- 卷积same:f=5, padding=2,filters=256,图像变为27x27x256
- 最大池化:f=3, s=2,图像变为13x13x256
- 卷积same:f=3, padding=1, filters=384,图像变为13x13x384
- 卷积same:f=3, padding=1, filters=384,图像维度不变
- 卷积same:f=3, padding=1, filters=256,图像变为13x13x256
- 最大池化:f=3, s=2,图像变为6x6x256
- 全连接层:9216 -> 4096
- 全连接层:4096 -> 4096
- 分类输出:softmax分为1000类
共计约6000万个参数,使用ReLU作为激活函数,
VGG-16

- 输入:224x224x3的图片
- 卷积网络
- 卷积:f=3, s=1, same
- 最大池化:f=2, s=2
- 重复16次
- 全连接层
- softmax
共计约1.38亿参数,每一组卷积层后,图像缩小一倍,通道数量翻倍。
ResNet

残差块
ResNet网络是由残差块构成的。
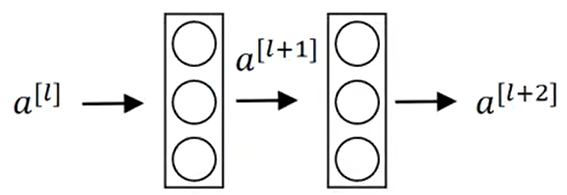

这样$a^{[l+2]}=g(z^{[l+2]}+a^{[l]})$
ResNet的意义
对于没有残差连接的普通神经网络而言,网络越深,优化算法越难训练,并且随着网络深度的加深,训练错误会越来越多。
如果有了ResNet,即使网络深度很深,错误率也不会上升。
为什么ResNet有效
如果在很深的网络处,有某层网络出现了梯度消失的问题,即W=0。
根据$a^{[l+2]}=g(z^{[l+1]}+a^{[l]})=g(w^{[l+2]}a^{[l+1]}+b^{[l+2]}+a^{[l]})$
由于梯度消失,$w^{[l+2]}=0$,此时若$b^{[l+2]}=0$,则$a^{[l+2]}=g(0+0+a^{[l]})=g(a^{[l]})$,因为激活函数是ReLU函数,$a^{[l]}$已经激活过,因此$a^{[l+2]}=g(a^{[l]})=a^{[l]}$。
这样就相当于跳过了梯度消失的部分。
Inception网络
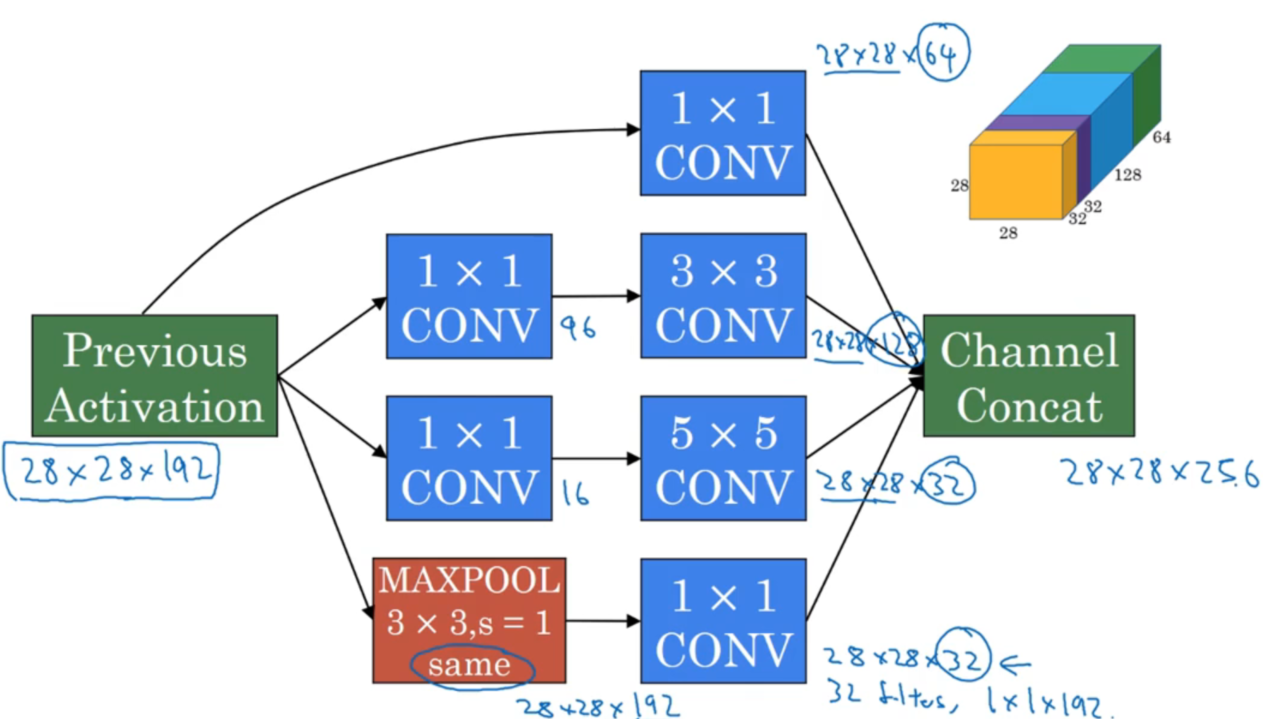
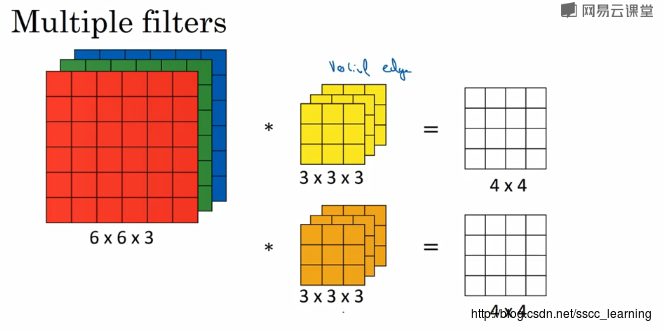
上图为Inception模块,原理就是将不同卷积核卷积出的结果,按通道叠加连接成一个具有所有卷积特征的大方块。
由于提供了各种不同的卷积核,因此网络训练时可以自动选择效果最好的一种或几种卷积核组合,避免了使用单一类型的卷积核的限制。

这是Inception网络的结构,其就是将传统的卷积层替换为了Inception模块。
评论