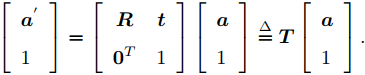相机模型与去畸变方法详解
相机我们都熟悉,可以将三维空间的点集映射到二维平面中。而这映射过程,就需要我们使用几何模型去描述。
最简单最基础的模型就是针孔相机模型,它描述了相机的基本投影与成像的惯性。
但是我们常用的相机都是存在透镜的,因为透镜的缘故,光线投影成像时就会产生畸变,这时就需要畸变模型进行更准确的描述了。
此外,在许多场合还会需要利用摄像头实现测距功能,因此这里也介绍了双目相机模型和RGB-D深度相机模型。
一、针孔相机模型
实际物体的各点转换为图像上像素的过程可概括为
① 首先获得世界坐标系下实际点的坐标
② 将世界坐标系的坐标转换成相机坐标系下的坐标
③ 相机坐标系的坐标映射为图像上的某一个像素点
1.1 成像原理
我们中学都做过小孔成像的物理实验,现实的空间点经过小孔投影后,在平面上会成一个倒立的像。而且实际点到光轴的距离X,与图像上对应点到中心的距离X’,其比值与实际点到小孔的垂直距离以及焦距有关。
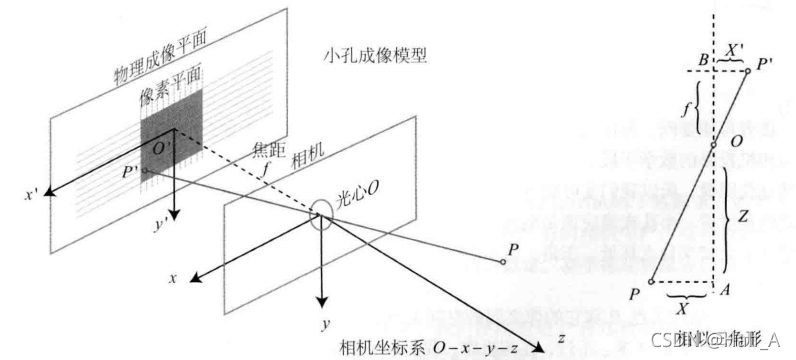
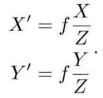
这样,我们可以在成像平面上可以得到真实物体的等比例放缩后的图像。不过相机中,我们最后获得的是一个个像素,因此还需要对所成的像进行采样和量化。
1.2 实际坐标与像素坐标的关系
我们设在成像平面上固定一个像素坐标系ouv,原点o在图像左上角,u轴与x轴同向平行,v轴与y轴反向平行。这样像素坐标系和物理成像之间差了一个缩放和原点的平移。设像素坐标在u轴缩放了α倍,在v轴缩放了β倍,则关系式如下:
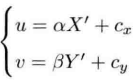
将两个等式中的X’和Y’用上面的关系式替换为X与Y的表达式
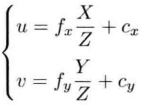
改写成矩阵形式更加简洁形象
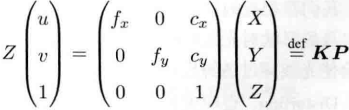
这样,就得到了实际点P与像素点(u,v)之间的对应关系,并且由中间量组成的矩阵称为相机的内参数矩阵K。这个内参数矩阵通常相机厂商会提供,如果没有则需要自己进行相机标定。
1.3 如何获得实际坐标
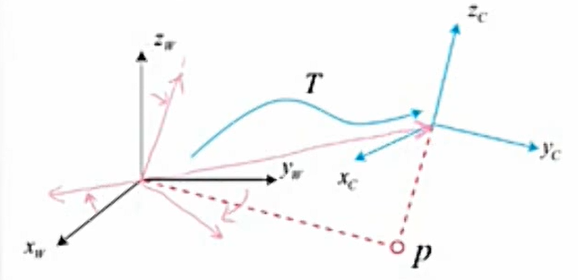
我们通常说的某个点的空间位置是以世界坐标系为基础描述的,但是在相机模型中,我们需要实际点相对于相机的位置关系。而且由于相机是在运动的,因此利用变化矩阵的相关知识可以得到下面的式子
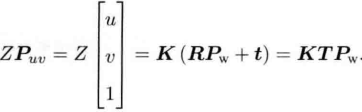
其中相机的R,t就是相机的外参,外参会随相机运动而变化,内参则不会发生改变。
二、畸变相机模型
2.1 两种常见畸变的介绍
实际的相机为了获得更好的成像效果,通常会在相机前方加入透镜,透镜的加入会使得光线传播收到影响,即真实世界的直线在图像中变成了曲线,这种叫径向畸变。径向畸变又分为桶形畸变和枕形畸变。
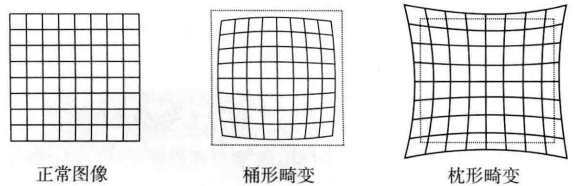
同时由于安装误差,透镜和成像平面不会完全平行,也会使投影位置发生变化,这种叫切向畸变。
2.2 去畸变方法
① 对于径向畸变
径向畸变可以看做坐标点沿长度方向发生了变化,即坐标点距离原点距离变了。通常使用的模型如下,假设畸变成多项式关系,使用三个参数k1, k2, k3表达畸变。
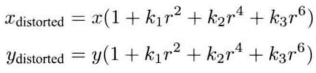
其中 [$x_{distorted}$, $y_{distorted}$] 是畸变后的点的归一化坐标。r表示点p与坐标系原点的距离。
② 对于切向畸变
切向畸变可以看做坐标点沿切线方向发生了变化,即水平夹角变了。通常使用p1, p2两个参数表达切向畸变,具体公式如下。
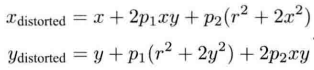
③ 综合方法
结合上面两种径向畸变和切向畸变的公式,可以得到综合的去畸变公式,也就是说我们通过五个畸变系数就可以确定点在像素平面的正确位置。
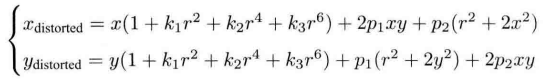
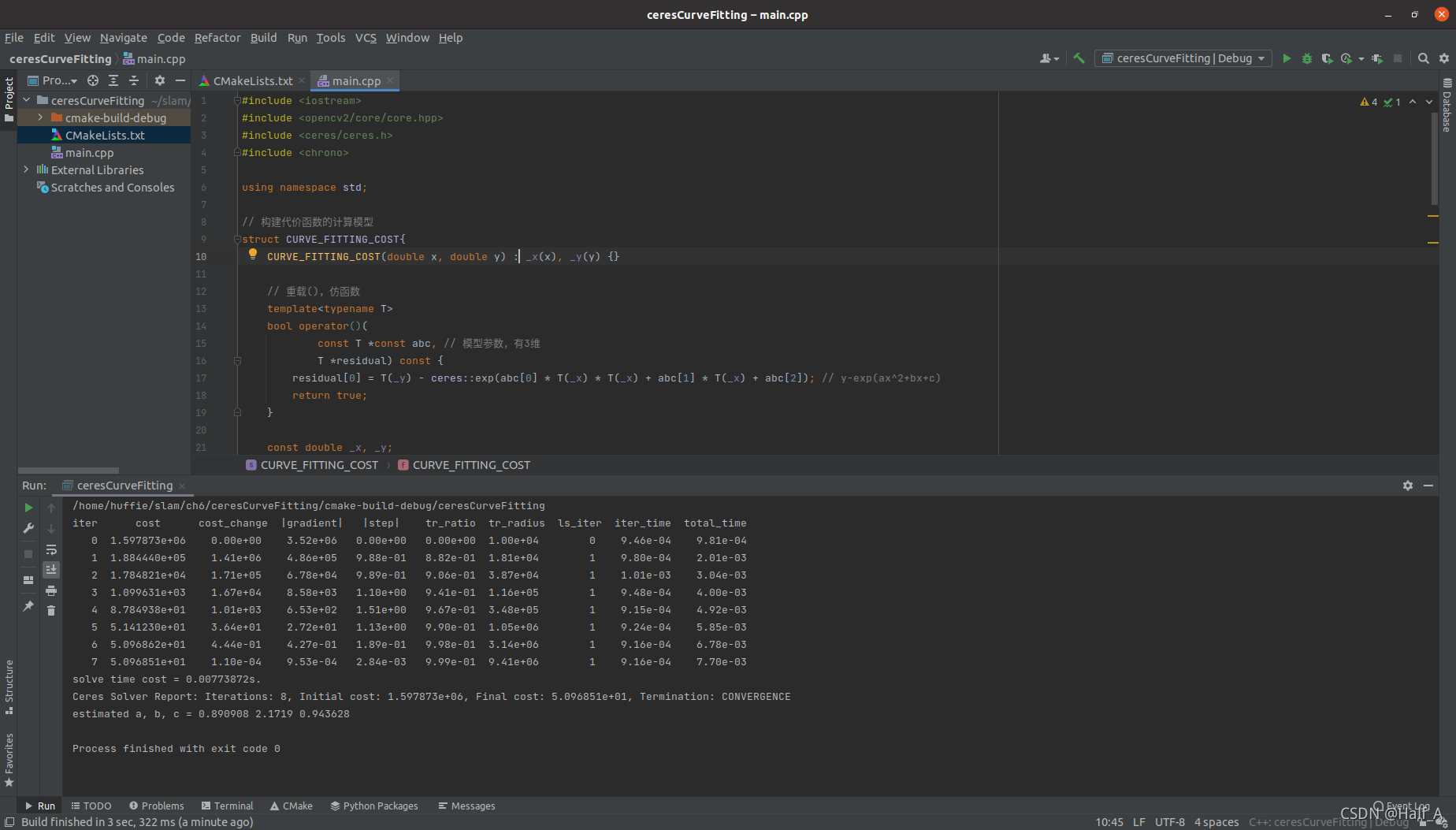
2.3 示例程序
1 |
|