【深度学习笔记04】改善训练效果与训练速度的一些要素
一、训练集、验证集和测试集
对于输入数据,我们通常将它分成几个部分:训练集、交叉验证集和测试集。
在先前机器学习的小数据量时代,通常将所有数据划分为60%训练集20%验证集,20%测试集。这是当时普遍认可的比较合理的方法。
但在大数据时代,验证集和测试集的比例会变小,例如对于一百万条数据,我们只需要一万条做验证集,一万条做测试集,即98%训练集,1%验证集,1%测试集。
选择数据时要确保验证集和测试集要来自同一分布。
二、偏差和方差
偏差过大时,会出现拟合曲线与实际值差值过大,即欠拟合现象。
方差过大时,会出现拟合曲线过于复杂,即过拟合现象。
训练集错误率远低于验证集错误率时,说明我们过拟合了训练集,没有充分利用交叉验证集的作用,这种情况即高方差情况。
训练集错误率和验证集的错误率都较高时,说明训练数据的拟合度不高,就是欠拟合现象,也就是高偏差情况。
训练集错误率
三、机器学习基础
首先我们要计算算法的偏差,如果偏差很高,纳闷我们可以选择一个新网络,选择更多的隐藏层,或者花费更多时间训练算法,扩大网络的规模,这些方法可能会起作用,可能不会。
然后评估算法的方差,如果方差高,最好的解决方法就是增加数据量,也可以使用正则化来减少过拟合。
当我们找到低偏差和低方差的算法,我们就成功做好了机器学习。
需要注意的是偏差和方差是两种不同的问题,需要采取不同的解决方法。
四、正则化
4.1 如何实现正则化
当神经网络存在过拟合现象,也就是出现高方差时,通常都会想到正则化。(另一个常用的方法是增大数据量)
对损失函数$J(w,b)$添加正则化:
$J(w,b)=\frac{1}{m}\sum^m_{i=1}l(\hat y^{(i)},y^{(i)})+\frac{\lambda}{2m}||w||_2^2$
其中$\frac{\lambda}{2m}||w||^2_2$就是正则项,也称为$L_2$正则化(由于利用了$||w||^2$),这种正则化方式也是应用最多的方式。$L_1$正则化项为$\frac{\lambda}{2m}\sum^{n_x}_{j=1}|w_j|$。
$\lambda$为正则化参数,我们需要使用验证集来配置这个参数,尝试各种各样的数据集来调整参数,因此$\lambda$是一个超参数。
在神经网络中:
$J(w^{[1]}, b^{[1]}\dots w^{[L]}, b^{[L]})=\frac{1}{m} \sum^n_{i=1}l(\hat y, y)+\frac{\lambda}{2m}\sum^L_{l=1}||w^{[l]}||^2_F$
其中$||w^{[l]}||^2_F=\sum^{n^{[l-1]}}{i=1}\sum^{n^{l}}{j=1}(w_{ij}^{[l]})^2$,称为Frobenius norm,是矩阵中所有元素的平方求和。
在计算梯度时会计算$\frac{\partial J}{\partial w}$,因此求出来的梯度会在原有基础上多一个正则项:
$dw^{[l]}=(backprop)+\frac{\lambda}{m}w^{[l]}$
所以在参数更新时,也会附加一个正则项
$w^{[l]}=w^{[l]}-\alpha[(backprop)+\frac{\lambda}{m}w^{[l]}]$
相当于对参数更新的速度进行缩小,因此$L_2$正则化也称为权重衰减。
4.2 为什么正则化可以减少过拟合
添加正则化后,可以避免权值矩阵过大。
直观上理解就是如果正则化参数$\lambda$设置的足够大,权重矩阵就会被设置为接近0的值,于是就消除了这些隐藏单元的许多影响,因此整个神经网络就变成了类似于有许多隐藏层,但每个隐藏层只有一个隐藏单元的高偏差情况。
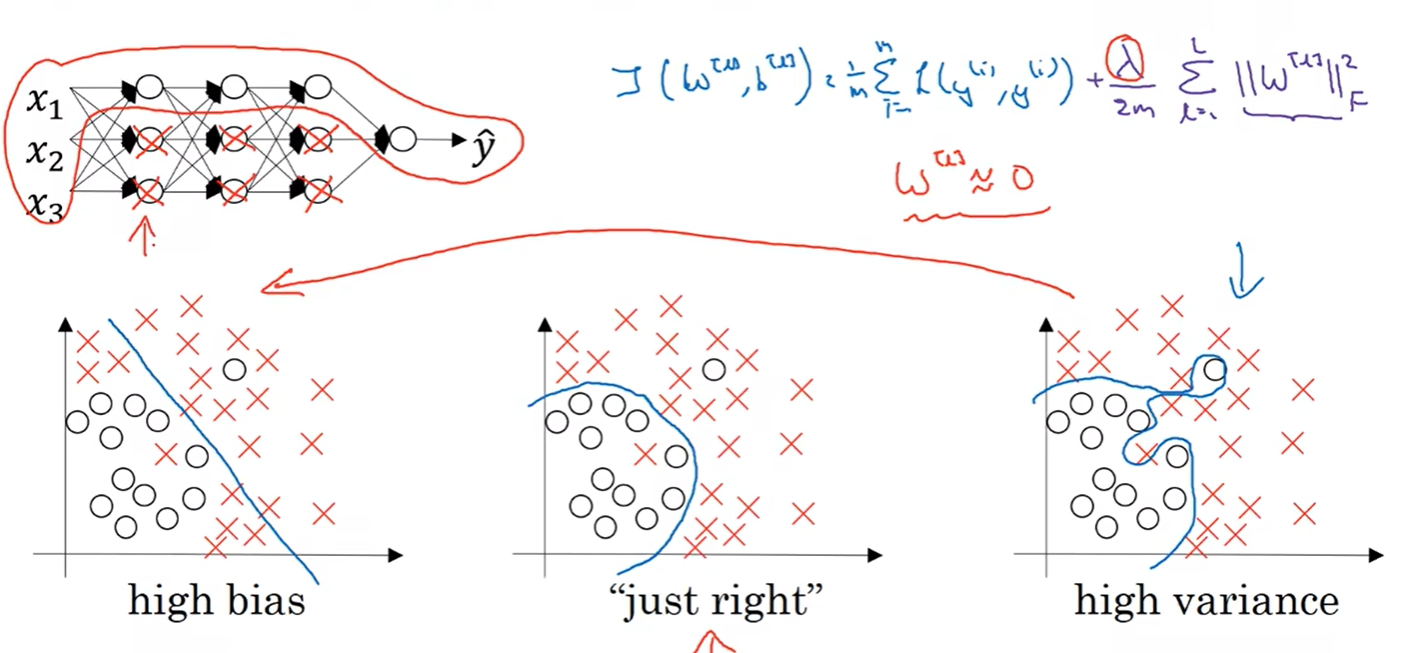
另一方面,当权重矩阵W变小时,$Z=Wa+b$也会变小,因此对于类似于tanh的激活函数来说,$g(z)$就会落在靠近y轴两侧的近线性区域,简化了模型,更不容易出现过拟合。
4.3 Dropout正则化
Dropout会遍历网络的每一层,并为每一层设置消除或保留神经节点的概率,设置完后,会在每一层消除一些节点。然后用反向传播训练精简后的模型,对于所有样本,我们都随机设置概率。
(1)如何实现Dropout正则化
最常用的方法是反向随机激活。
以一个三层网络举例,首先定义向量d3=np.random.rand(a3.shape[0], a3.shape[1]),即d3与a3同纬度。
比较d3<keep.prob,表示保留隐藏单元的概率。将d3中各个元素小于keep.prob的设置为1,大于keep.prob设置为0。
然后过滤d3中所有等于零的元素,a3=np.multiply(a3,d3)。
向外扩展a3,a3/=keep.prob,主要是为了保证$Z=Wa+b$中的Z期望值不变,由于消除了a中的80%的元素,因此将剩余元素扩大1/0.8倍,Z的期望不变。
(2)如何理解Dropout正则化
对于每一个神经元节点来说,它的输入特征(上一层的节点)随时都有可能消除,因此不能依赖任何一个特征,因此将不会在某一个输入上加太多的权重,因此会对所有输入同等看待。
并且,不同的层其keep.prob值也不一样,对于可能出现过拟合的层,可以设置keep.prob值比其他层更低。
dropout算法通常应用在计算机视觉领域,其他学科应用的不是那么广泛。
由于每次迭代都会随即删除一些节点,因此很难评价J,J将不会是单调递减情况,通常情况下会先关闭dropout正则化,再调试好J为单调递减后,在开启。
4.4 其他正则化
(1)数据增广
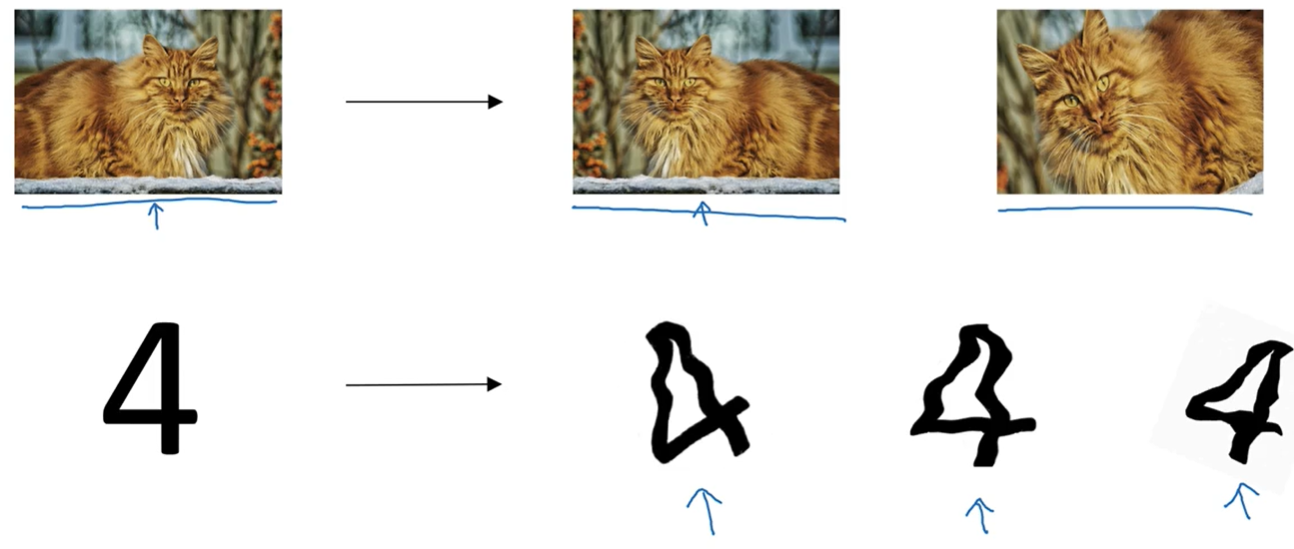
对于图片分类情况来说,如果我们想要扩展数据集,可以采用如翻转图片、旋转图片、放缩裁剪图片等方法,并添加到数据集中,虽然这种方法不如采集新数据有效,但对于消除过拟合仍然有作用。
(2)提前终止
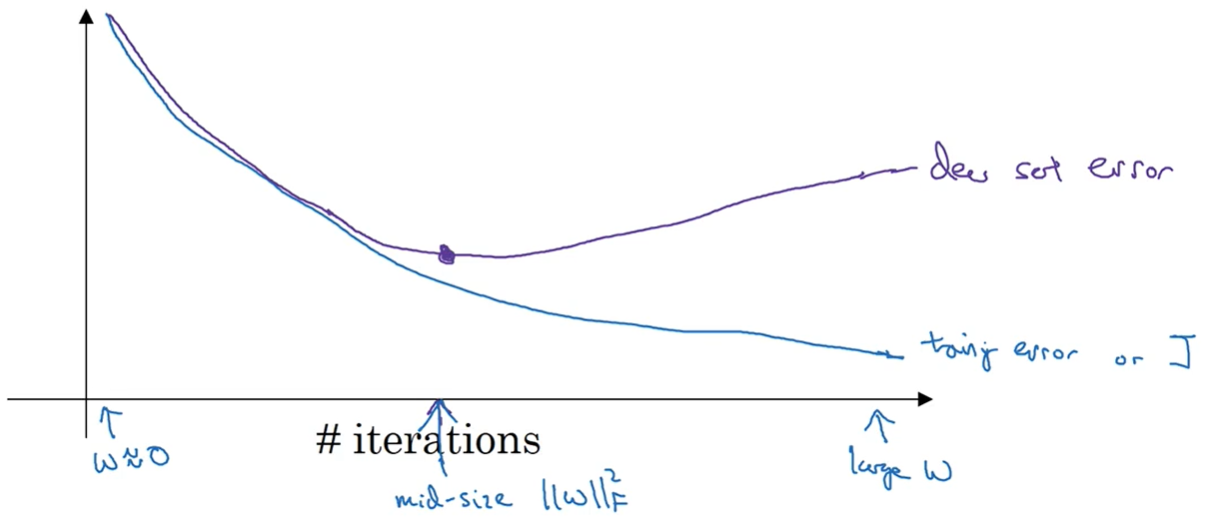
当运行梯度下降时,我们可以绘制出损失函数的曲线(通常是单调递减的),也可以绘制验证集上的误差,通常会发现,验证机误差是先下降再上升的,这个时候我们可以找到验证集误差最小的地方,然后停止迭代。
五、归一化
假设有一个训练集,有两个输入,归一化输入有两个步骤
(1)零均值化
$\mu=\frac{1}{m}\sum^m_{i=1}x^{(i)}$
$x=x-\mu$
(2)归一化
$\sigma^2=\frac{1}{m}\sum^m_{i=1}x^{(i)^2}$
$x/=\sigma$
这样之后x1和x2就是以0为中心,方差为1的数据集。
(3)为什么要标准化
如果两个输入特征的值差距很大,那么得到的权值矩阵W1和W2中的值差距也会很大,这就会导致损失函数的梯度曲线十分不均匀,需要将学习率设置为非常小才能得到最优解。
相反如果归一化后,那么无论从哪个位置开始,都可以很好的梯度下降到最优解。

六、梯度消失与梯度爆炸
对于一个有很深很深层的神经网络来说,它的预测值$\hat y$可能是这样的:
$\hat y=w^{[l]}+w^{[l-1]}+\dots+w^{[3]}+w^{[2]}+w^{[1]}$
这样就会导致如果每一层的w大于1,那么$\hat y$以及梯度$dw$等的值就会爆炸式增长,如果每一层的w小于1,那么$\hat y$的值就会指数级下降。
七、权重初始化
对于某一个节点来说,如果它的输入特征过多,例如:
$z=w_1x_1+w_2x_2+\dots+w_nx_n$
那么随着输入特征数量n越多,每一个权值$w_i$就越小。
因此通常的做法会将每一个$w_i$变小为$\frac{1}{n}$倍,实际中采用以下做法
$W^{[l]}=np.random.randn(shape)*np.sqrt(\frac{2}{n^{[l-1]}})$
对于ReLU激活函数,最右侧使用$np.sqrt(\frac{2}{n^{[l-1]}})$
对于tanh激活函数,最右侧使用$np.sqrt(\frac{1}{n^{[l-1]}})$,或者$np.sqrt(\frac{2}{n^{[l-1]}+n^{[l]}})$
也可以将分子的1或者2作为一个超参数进行调整,虽然作用不大就是了。
八、梯度检验
注意梯度检验只用于debug环节,实际训练时不要开启此功能,因为它运算太慢了。
假设网络中含有以下参数:$W^{[1]},b^{[1]}\dots W^{[l]},b^{[l]}$
首先要将所有参数矩阵转换成向量并连接起来,形成一个巨大的向量$\theta$。
因此$J(W^{[1]},b^{[1]}\dots W^{[l]},b^{[l]})=J(\theta)$
同样获得一个巨大的梯度向量$d\theta$。
(1)计算近似梯度
$d\theta_{approx}[i]=\frac{J(\theta_1,\theta_2,\dots,\theta_i+\epsilon,\dots)-J(\theta_1,\theta_2,\dots,\theta_i-\epsilon,\dots)}{2\epsilon}$
其中的$\epsilon$通常取$10^{-7}$
(2)计算近似梯度与所求梯度的距离
通常采用欧几里得距离$\frac{||d\theta_{approx}-d\theta||2}{||d\theta{approx}||+||d\theta||}$
如果计算出来的距离大约为$10^{-7}$,说明没问题,如果过大比如$10^{-5}$,说明其中某个环节可能存在问题,可以对逐个i计算,看看是哪个环节存在问题。