简单理解时间复杂度
关于代码执行次数
给出一段代码,这段代码的总执行次数可以用T(n)表示,其中n是输入数据的大小或数据量,T(n)是在输入数量为n时,某段代码的总执行次数。
以下面两段代码为例:
1 | int func1(void) |
该段代码的执行次数为T(n)=2
(两条语句各执行一次)
1 | int func2(int n) |
该段代码的执行次数为T(n)=3n+3
(int i = 0执行1次,i<n执行n+1次,i++执行n次,printf执行n次,return执行1次)
但实际中一般不会一条一条语句去数,而是采用估算。
时间复杂度
代码执行次数的简化估算值就是时间复杂度。
如何通过代码执行次数得到时间复杂度
代码执行次数T和时间复杂度O的简化估算关系如下:
| 代码执行次数T | 时间复杂度O |
|---|---|
| 常数 | O(1) |
| 常数 × n + 常数 | O(n) |
| 常数 × n^2 + 常数 × n + 常数 | O(n^2) |
| 常数 × n^a + 常数 × n^(a-1) … | O(n^a) |
例如,如果T(n)=常数,那么时间复杂度可以估算为1。
例如,对于多项式,只选取最高此项并忽略系数,因为低次项的增长远远不及最高次项
常见代码的时间复杂度
常规情况
(1)没有循环
时间复杂度:O(1)
(2)有一重循环
时间复杂度:O(n)
(3)有二重循环
时间复杂度:O(n^2)
(4)有多重循环
时间复杂度:O(n^a)
其中a为循环层数
(5)有多个循环
时间复杂度:O(n^a)
其中a为层数最多的循环层数
(6)if…else…嵌套循环
以时间复杂度最多的分支计算
特殊情况
(1)i成比例增长
1 | void func(int n) |
代码总执行次数:T(n)=3log2(n)+2
时间复杂度:O(log(n))
时间复杂度的意义
时间复杂度不同,随着输入数据量的增加,代码运行的时间也会增加。
例如O(1)无论输入数据如何增多,代码运行时间都不变。而O(n)的运行时间和输入数据量成正比。如果时间复杂度过高,例如O(2^n),那么在小数据情况下,代码还可以运行,一旦数据量增大,则代码的运行时间将会几何级增加。
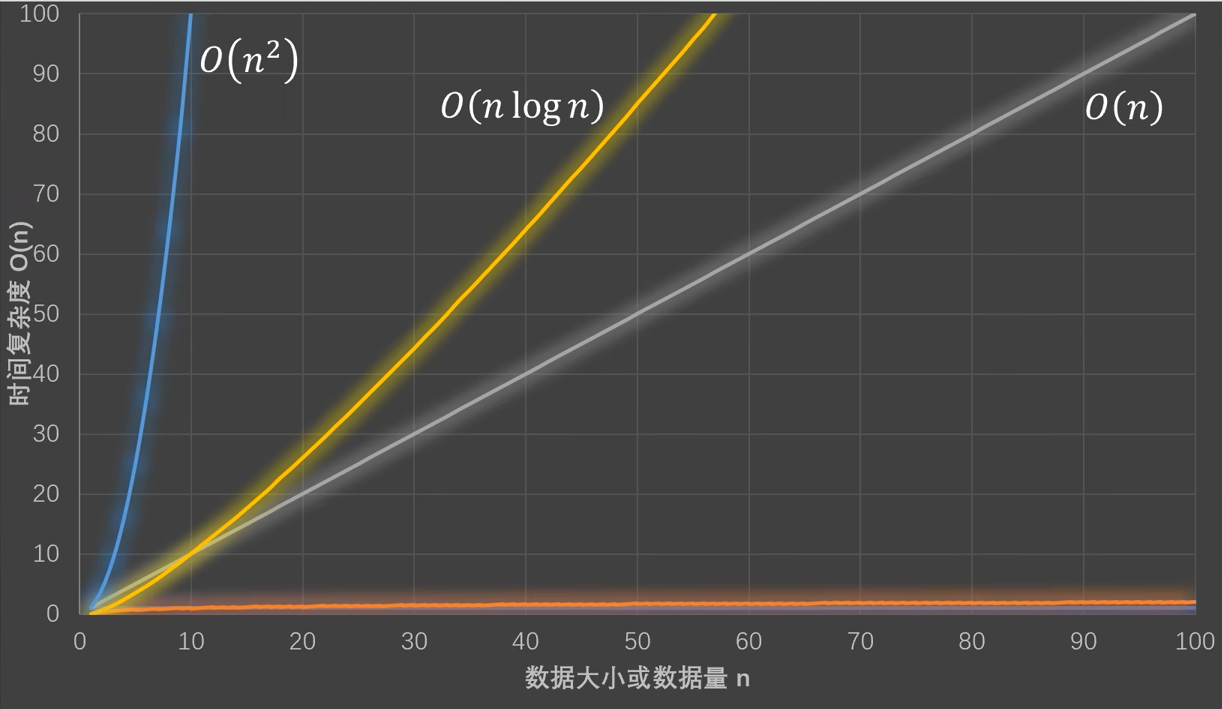
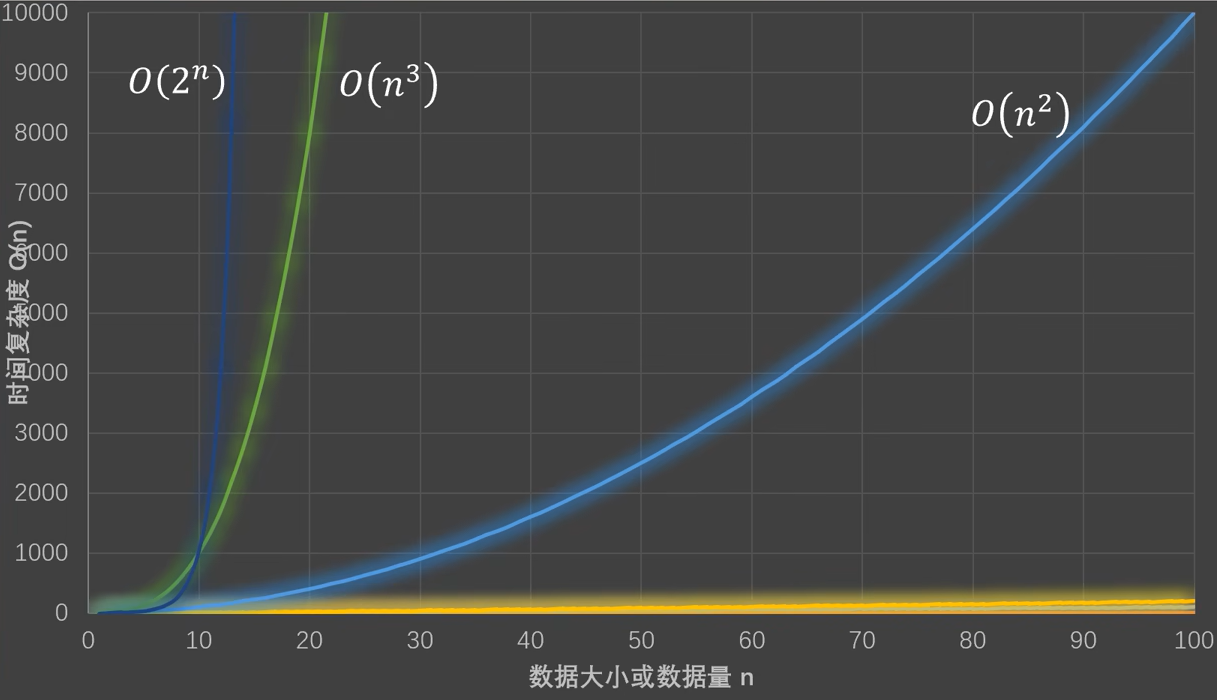
代码执行时间总结如下:
| 名称 | 时间复杂度 |
|---|---|
| 常数时间 | O(1) |
| 对数时间 | O(log n) |
| 线性时间 | O(n) |
| 线性对数时间 | O(nlog n) |
| 二次时间 | O(n^2) |
| 三次时间 | O(n^3) |
| 指数时间 | O(2^n) |
评论