一、卷积运算
前面已经提到,对于一个神经网络来说,例如人脸识别,前面的层主要用来提取图像的边缘,中间的层主要用来检测部分如眼睛鼻子嘴等,后面的层主要用来检测整个人脸。
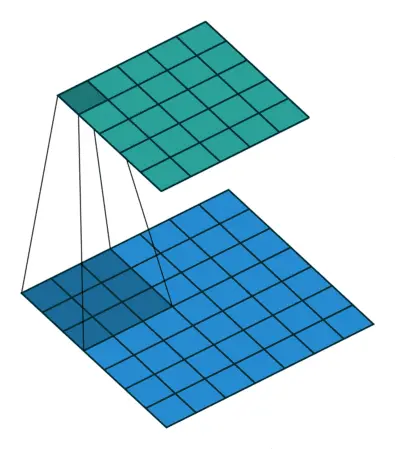
1.1 如何检测边缘
通常使用不同的卷积核或者称过滤器来实现各种边缘检测。
(1)垂直边缘
使用如下的卷积核进行检测:
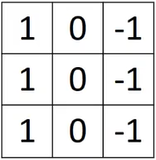
例如,对于一张具有垂直边缘的图像,利用此卷积核进行卷积运算,输出结果在边缘处数值较大,在图像变化缓慢的区域数值较小。
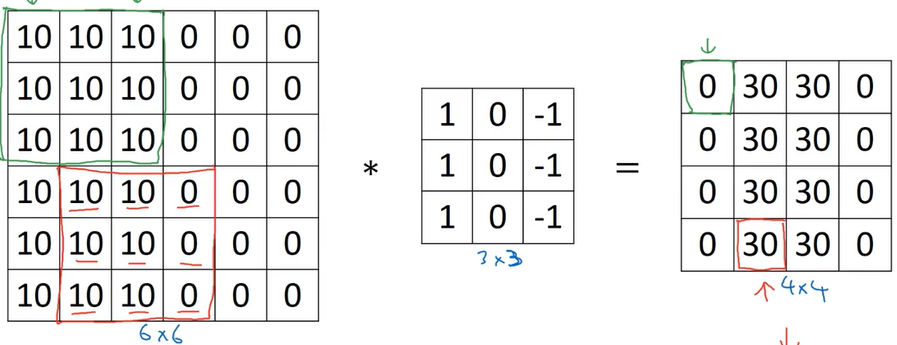
上面的卷积运算可以很好的计算出图像中边缘在什么位置,并且,如果卷积的结果是正值,说明从左到右是从亮到暗的变化,如果是负值,说明从左到右是从暗到亮的变化。
(2)水平边缘
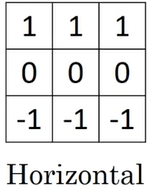
此卷积核可以计算图像的水平边缘,并且正值代表上方亮下方暗,数值越大边缘变化越明显。
(3)其他滤波器
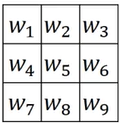
通过定义卷积核中的值的分布,可以实现检测不同方向的,不仅是水平竖直,也可以是45°75°。
此外还可以改变各行的数值,例如1:2:1,来实现更有目标的检测。
1.2 Padding
(1)普通卷积存在的问题
- 图像缩小:对于一个(n, n)的图像,使用(f, f)的卷积核做卷积,得到的图像大小是(n-f+1, n-f+1),因此每做一次卷积,图像大小都会减小。
- 边缘信息丢失:图像角落的像素只会被一个卷积核处理,边缘像素相比于中间的像素,也会容易丢失很多信息。
(2)解决方法
在进行卷积操作之前,先在图像边缘填充一层像素。
例如在图像边缘添加p层像素,那么卷积后图像大小是(n+2p-f+1, n+2p-f+1)。
通常情况下,卷积核边长是奇数
1.3 卷积步长
使用一个(f, f)的卷积核,卷积一个(n, n)的图像,padding为p,步长为s,输出的图像维度为$(\frac{n+2p-f}{s}+1, \frac{n+2p-f}{s}+1)$
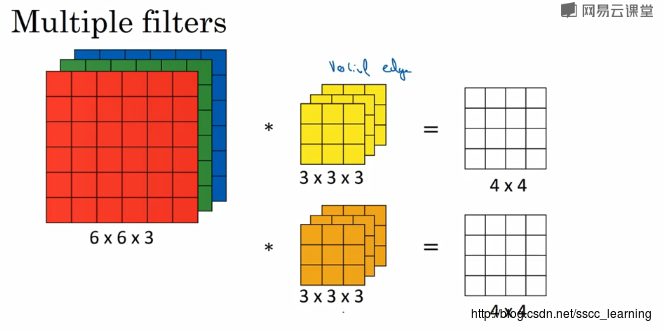
二、三维卷积
2.1 三维卷积基础
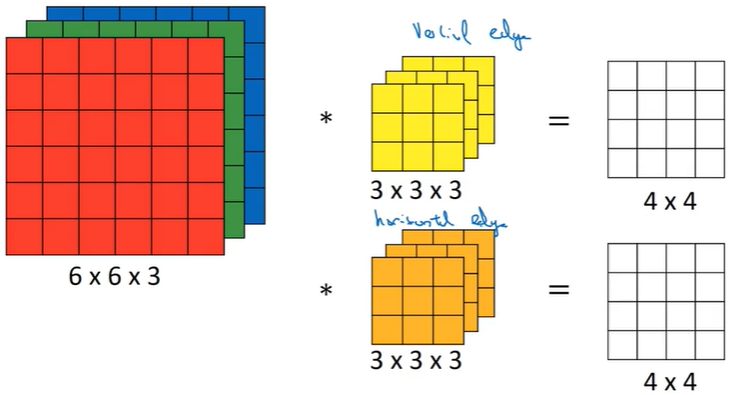
例如对于一个RGB图像来说,其有(w, h, 3)的维度,对其进行卷积,必须是(f, f, 3)的维度。
即图像和卷积核的通道数要相同。
卷积完成后的输出图像是(w-f+1, h-f+1, n)的n通道图像,其中n是卷积核的个数。
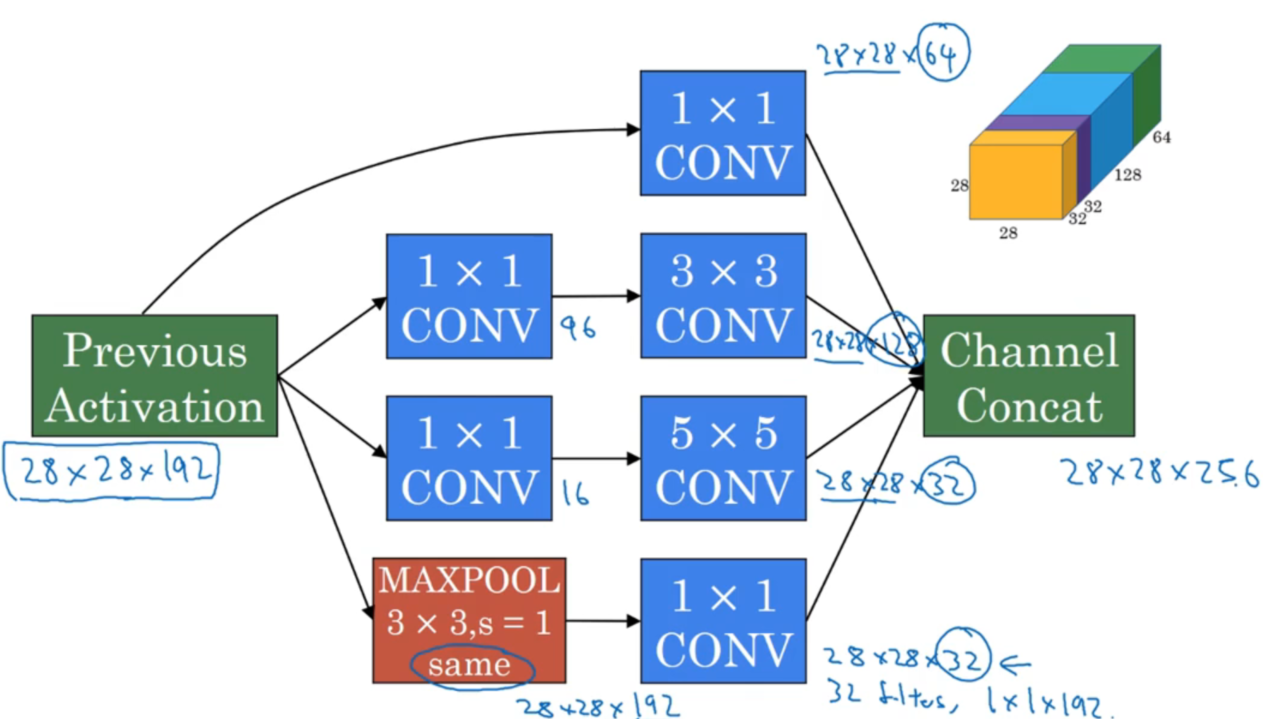
2.2 三维卷积在神经网络的应用
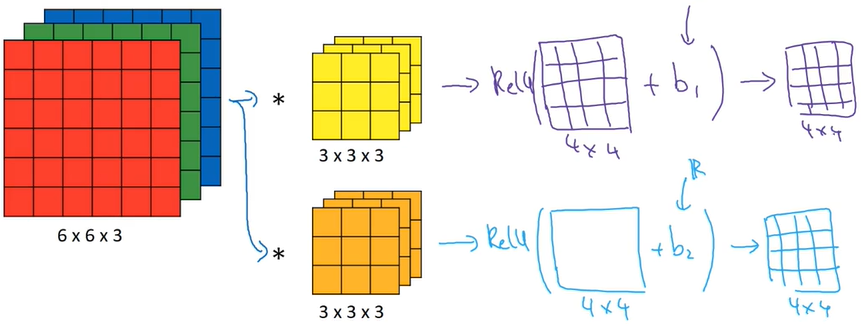
三维卷积在神经网络的应用,与传统方法基本一致。
在传统方法中有,$z^{[1]}=w^{[1]}a^{[0]}+b^{[1]}$,其中$a^{[0]}$就是输入x,$a^{[1]}=g(z^{[1]})$
而若是卷积运算,则只需将输入图片替换x,卷积核替换w,然后同样添加偏差和非线性激活函数即可。
三、池化层
池化层可以缩小模型大小,提高运算速度,提高模型的鲁棒性。
3.1 最大池化
例如对一个4x4的输入,最大池化选择2x2,那么输出就是将4x4的输入分成4部分,每部分取最大值填充到2x2中。最大池化输出维度的计算方法与卷积相同。
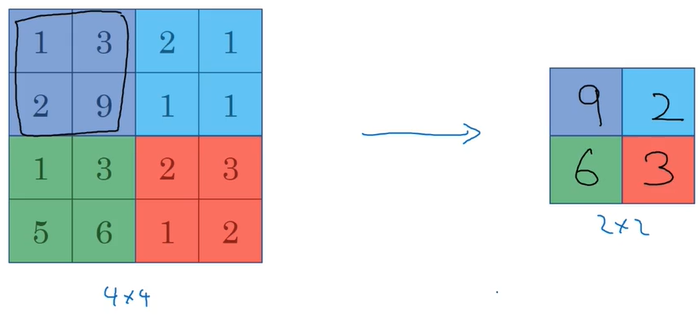
最大池化的作用是,如果卷积过滤提取到了某个特征,那么保留其最大值,如果没有提取到特征,那么最大值也还是很小。
3.2 平均池化
平均池化与最大池化类似,是在不同区域内求平均值,主要用在很深的网络。
目前来说最大池化比平均池化更常用。
3.3 池化总结
池化的参数主要有:
由于池化层没有权重,只有上面一些超参数,因此一般来说会将卷积层和池化层合并称为一层。
四、全连接层
在神经网络的最后,经过多轮的卷积和池化处理,最后的输出往往是宽高较小,通道数较多。这是我们会将其展开成为一个向量,这个向量的长度就等于上一层输出的$w\times h\times c$,将向量中的所有参数作为同样数量单元的输入,进行常规神经网络计算,这就是全连接层。
五、代码实现
(1)添加padding
1
2
3
4
5
6
7
8
9
10
11
12
13
| def zero_pad(X, pad):
"""
对数据集X的所有图像添加pad,padding被应用再一张图片的宽和高方向上。
参数:
X -- numpy数组,shape (m, n_H, n_W, n_C) 代表批量为m的图片
pad -- 整数,图片边缘填充的pad大小
Returns:
X_pad -- 添加了以0填充的pad图片,shape (m, n_H + 2*pad, n_W + 2*pad, n_C)
"""
X_pad = np.pad(X, ((0, 0), (pad, pad), (pad, pad), (0, 0)))
return X_pad
|
(2)单步卷积(numpy实现)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
| def conv_single_step(a_slice_prev, W, b):
"""
在上一层的一个切片用卷积核W进行卷积, 并添加偏差b
参数:
a_slice_prev -- 输入数据的切片,shape (f, f, n_C_prev)
W -- 权重参数,以卷积核的形式体现,shape (f, f, n_C_prev)
b -- 偏置参数,shape (1, 1, 1)
返回值:
Z -- 标量,滑动窗口(W, b)与输入切片x的卷积计算的结果
"""
S = np.multiply(W, a_slice_prev) + b
Z = np.sum(S)
return Z
|
(3)三维卷积(numpy实现)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
| def conv_forward(A_prev, W, b, hparameters):
"""
卷积前向计算
参数:
A_prev -- 上一层的激活输出,shape (m, n_H_prev, n_W_prev, n_C_prev)
W -- 权重, shape (f, f, n_C_prev, n_C)
b -- 偏置, shape (1, 1, 1, n_C)
hparameters -- 包含 "stride" 和 "pad" 的字典
返回值:
Z -- 卷积输出,shape (m, n_H, n_W, n_C)
cache -- 缓存,用于conv_backward()函数
"""
m, n_H_prev, n_W_prev, n_C_prev = A_prev.shape
f, _, n_C_prev, n_C = W.shape
stride = hparameters["stride"]
pad = hparameters["pad"]
n_H = (n_H_prev - f + 2 * pad) // stride + 1
n_W = (n_W_prev - f + 2 * pad) // stride + 1
n_C = W.shape[3]
Z = np.zeros((m, n_H, n_W, n_C))
A_prev_pad = zero_pad(A_prev, pad)
for e in range(m):
A_prev_pad_e = A_prev_pad[e]
for h in range(n_H):
for w in range(n_W):
for c in range(n_C):
vert_start = h * stride
vert_end = vert_start + f
horiz_start = w * stride
horiz_end = horiz_start + pad
A_prev_pad_slice = A_prev_pad_e[vert_start:vert_end, horiz_start:horiz_end, :]
Z[e, h, w, c] = np.sum(np.multiply(A_prev_pad_slice, W[:, :, :, c]) + b[:, :, :, c])
assert(Z.shape == (m, n_H, n_W, n_C))
cache = (A_prev, W, b, hparameters)
return Z, cache
|
(4)池化
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
|
def pool_forward(A_prev, hparameters, mode = "max"):
"""
前向传播的池化层
参数:
A_prev -- 输入数据,shape (m, n_H_prev, n_W_prev, n_C_prev)
hparameters -- 包含 "f" 和 "stride" 的python字典
mode -- 想要使用的池化模式, 定义为字符串 ("max" or "average")
返回值:
A -- 池化层输出,shape (m, n_H, n_W, n_C)
cache -- 保存池化层的数据,用于反向传播
"""
(m, n_H_prev, n_W_prev, n_C_prev) = A_prev.shape
f = hparameters["f"]
stride = hparameters["stride"]
n_H = int(1 + (n_H_prev - f) / stride)
n_W = int(1 + (n_W_prev - f) / stride)
n_C = n_C_prev
A = np.zeros((m, n_H, n_W, n_C))
for e in range(m):
for h in range(n_H):
for w in range(n_W):
for c in range(n_C):
vert_start = h * stride
vert_end = vert_start + f
horiz_start = w * stride
horiz_end = horiz_start + f
A_prev_slice = A_prev[e, vert_start:vert_end, horiz_start:horiz_end, c]
if mode == "max":
A[e, h, w, c] = np.max(A_prev_slice)
elif mode == "average":
A[e, h, w, c] = np.mean(A_prev_slice)
cache = (A_prev, hparameters)
assert(A.shape == (m, n_H, n_W, n_C))
return A, cache
|