【深度学习笔记06】参数调试处理
一、超参数的取值
需要处理的参数通常包括:
| 参数 | 常用取值范围 | 调试重要度 |
|---|---|---|
| 学习率$\alpha$ | 0.1 | 最重要 |
| 动量 | 0.9 | 重要 |
| 优化参数$\beta_1,\beta_2,\epsilon$ | $\beta_1=0.9,\beta_2=0.999,\epsilon=10^{-8}$ | 一般不修改 |
| 层数layers | 一般 | |
| 隐藏单元数hidden units | 重要 | |
| 学习率衰减learning rate decay | 一般 | |
| 批量大小mini-batch size | 重要 |
如何调试选择参数:
- 首先大范围随机选择参数,根据随机取点测试超参数的效果,确定影响最大的参数是哪个。因为对于实际问题而言,很难确定哪个超参数对结果的影响更大,在众多参数中如果一个一个测试往往找不到需要调试的参数。
- 采用由粗糙到精细的策略,找到随机测试中结果较好的参数范围,然后放大这一范围,在其中更密集的取值测试,搜索超参数的最优选择。
如何有效的随机取值
例如在搜索学习率$\alpha$的取值,其取值可能范围是0.0001-1。如果使用常规的随机取值,那么取到的值将有90%在0.1-1,只有10%在0.0001-0.1,而实际情况是学习率在后者的可能性更大。
为了解决这个问题,可以采用对数轴。在对数轴上随机取值,这样就可以保证在0.0001-0.1的取值数量大幅增加。
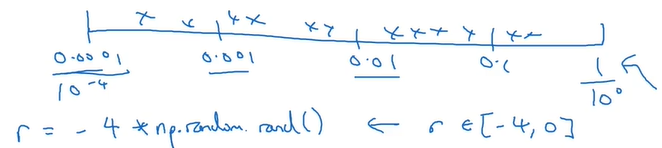
又例如在搜索动量$\beta$的值,其取值范围可能是0.9-0.999,但是实际取值肯定会更接近0.9,因此也可以使用上面的方法,通过用上面的方法取$1-\beta$的值[0.001,0.1],来间接取$\beta$的值。
关于为什么要采用非线性轴取值?因为超参数在不同的范围,对结果的灵敏度不同,以动量$\beta$为例,其在0.9变化为0.9001,比从0.999变为0.9991,对结果的影响要大很多。因此需要更多的在灵敏度高的区间取值,故采用了非线性轴取值方法。
二、Batch-Normalization(BN)
2.1 BN的基本思路
在logistic回归中,我们使用了归一化方法(计算平均值、方差),改善了训练样本,加快了梯度下降的速度。
但在深层网络中,下一层做梯度下降的数据是上一层网络的输出结果。实际中会将上一层的数据,在激活之前进行归一化,然后再激活,传递给下一层。
在神经网络中,假设有一些隐藏单元值$z^{(1)}\dots z^{(m)}$,计算:
$\mu=\frac{1}{m}\sum_i z^{(i)}$
$\sigma^2=\frac{1}{m}\sum_i(z_i-\mu)^2$
$Z^{(i)}_{norm}=\frac{z^{(i)}-\mu}{\sqrt{\sigma^2+\epsilon}}$
这样就实现了将每层网络的输出z进行了标准化,这时输出就是平均值0和方差1的数据,我们虽然想通过正则化规范数据,加快梯度下降,但我们不想让它们都服从同样均值和方差的分布,因此有了下面的变式:
$\widetilde z^{(i)}=\gamma z_{norm}^{(i)}+\beta$
这里的$\gamma,\beta$是新的超参数,作用是设置输出z的平均值和方差。
2.2 BN为何有效
BN可以使权重比网络更滞后或更深层。
对于神经网络的某一层而言,其输入数据就是上一层的输出,由于随着参数的更新,上一层的输出是实时变化的,这就导致当前层的训练总是面对不同分布的输入。
使用BN后,可以将上一层的数据归一化到同一分布中,使上一层的输出数据更加稳定,进而保证之后的层有更好的基础。
总而言之,BN减弱了前层参数的作用与后层参数作用之间的联系,使网络每层都可以自己学习,稍微独立于整个网络,这样有助于加速整个网络的学习。
三、Softmax
3.1 softmax数学表示
前面提到的分类方法都是用于二分分类,而softmax回归则适用于多种分类。常用C表示输入类别个数,也等于输出层单元数。
使用时就是将最后一层的激活函数换成softmax。
例如设网络的最后一层为$l$,则该softmax层计算过程如下:
计算线性部分:
$z^{[l]}=w^{[l]}a^{[l-1]}+b^{[l]}$
计算临时变量:
$t=e^{z^{[L]}}$
计算输出,也就是各个分类的概率:
$a^{[l]}=\frac{t_i}{\sum t_i}$
假设$z^{[l]}$是一个(4,1)的向量,那么$t,a^{[l]}$的维度都是(4,1),其中$a^{[l]}$内的四个值就是四种分类的概率。
3.2 训练softmax网络
(1)损失函数
由于softmax的输出与分类个数相同,因此需要新的损失函数。
$l(\hat y,y)=-\sum_{j=1}y_jlog\hat y_j$
要想让损失函数尽量小,就需要让$log\hat y_j$尽可能大,也就是对应的概率尽可能大。
(2)梯度下降
关键步骤是对softmax层求导:
$dz^{[l]}=\hat y-y$