一、基本概念

1.1 专业术语

（1）状态（State）：状态可以被理解为当前环境的情况。

（2）动作（Action）：动作是智能体（agent）采取的行为。

（3）策略（Policy）：策略是用于在给定观测状态下做出决策的函数，通常表示为 $\pi(a|s)$，其中 $a$ 是动作，$s$ 是状态。强化学习的目标是学习策略函数，通常以概率密度函数的形式表示。

（4）奖励（Reward）：奖励定义了奖励的方式，对强化学习的结果产生重要影响。

（5）状态转移（State Transition）：状态转移表示在当前状态下，当智能体执行一个动作后，环境可能随机转移到的下一个状态的概率，通常表示为 $P(S’|S, A)$。

（6）回报（Return）：回报又被称为未来奖励的累积，通常表示为 $U_t = R_t + R_{t+1} + R_{t+2} + \ldots$。

（7）折扣回报（Discounted Return）：折扣回报考虑未来奖励的折扣效应，用折扣率 $\gamma$ 表示，通常表示为 $U_t = R_t + \gamma R_{t+1} + \gamma^2 R_{t+2} + \ldots$。

（8）动作价值函数（Action-Value Function）：动作价值函数表示在给定状态和动作下，智能体可以获得的期望回报，通常表示为 $Q_\pi(s_t, a_t) = E[U_t | S_t=s_t, A_t=a_t]$。最优策略下的动作价值函数被表示为 $Q^*(s_t, a_t) = \max_\pi Q_\pi(s_t, a_t)$，使用动作价值函数可以评估当前动作的质量。

（9）状态价值函数（State-Value Function）：状态价值函数表示在给定状态下，按照策略函数的预期回报，通常表示为 $V_\pi(s_t) = E_A[Q_\pi(s_t, A)]$。状态价值函数可以告诉我们当前状态的好坏程度。

（10）交叉熵（Cross Entropy）：交叉熵用于度量两个概率分布之间的差异，通常表示为 $H(\textbf p, \textbf q) = -\sum^m_{j=1}p_j\cdot \log(q_j)$。当两个概率分布相同时，交叉熵达到最小值。

1.2 强化学习的随机性

（1）Action动作的随机性

因为动作是根据策略函数随机抽样得到的，因此agent有可能做策略中的任何一种动作，虽然这些动作的概率有大有小，但是动作本身是随机的。

（2）State transitions状态转移的随机性

假定agent作出了一个动作，环境会用概率随机抽样，给出下一个状态。

1.3 强化学习如何控制agent

（1）如果有策略函数 $\pi(a|s)$

给定一个观测状态 $s_t$
利用策略函数从所有可能的动作中随机采样 $a_t~\pi(\cdot|s_t)$

（2）如果有最优的动作价值函数 $Q^(s,a)$

给定一个观测状态 $s_t$
最大化 $a_t=argmax_a Q^*(s_t,a)$ 来选择动作

二、价值学习 Deep Q-Network(DQN)

$U_t$ 反映未来奖励的总和，因此我们要知道 $U_t$ 的大小，由于其是一个随机变量，我们可以对 $U_t$ 求期望，只留下 $s_t$ 和 $a_t$ 两个变量。

$$Q_\pi(s_t,a_t)=E[U_t|S_t=s_t,A_t=a_t]$$

要想进一步消除策略函数 $\pi$，可以对 $Q_\pi$ 关于 $\pi$ 球最大化，记为 $Q^*$

$$Q^*(s_t,a_t)=max_\pi Q_\pi(s_t,a_t)$$

这个参数告诉我们不管在什么情况 $s_t$ 下做动作 $a_t$，那么期望顶多就是 $Q^*(s_t,a_t)$。

目标：完成任务（最大化总回报）
问题：如果已知 $Q^(s,a)$，那么最好的动作就是 $a^=argmax_a Q^(s,a)$，因为 $Q^$ 指示了该agent在s状态下选择a动作的好坏程度
挑战：我们不知道 $Q^*(s,a)$

（1）什么是 DQN

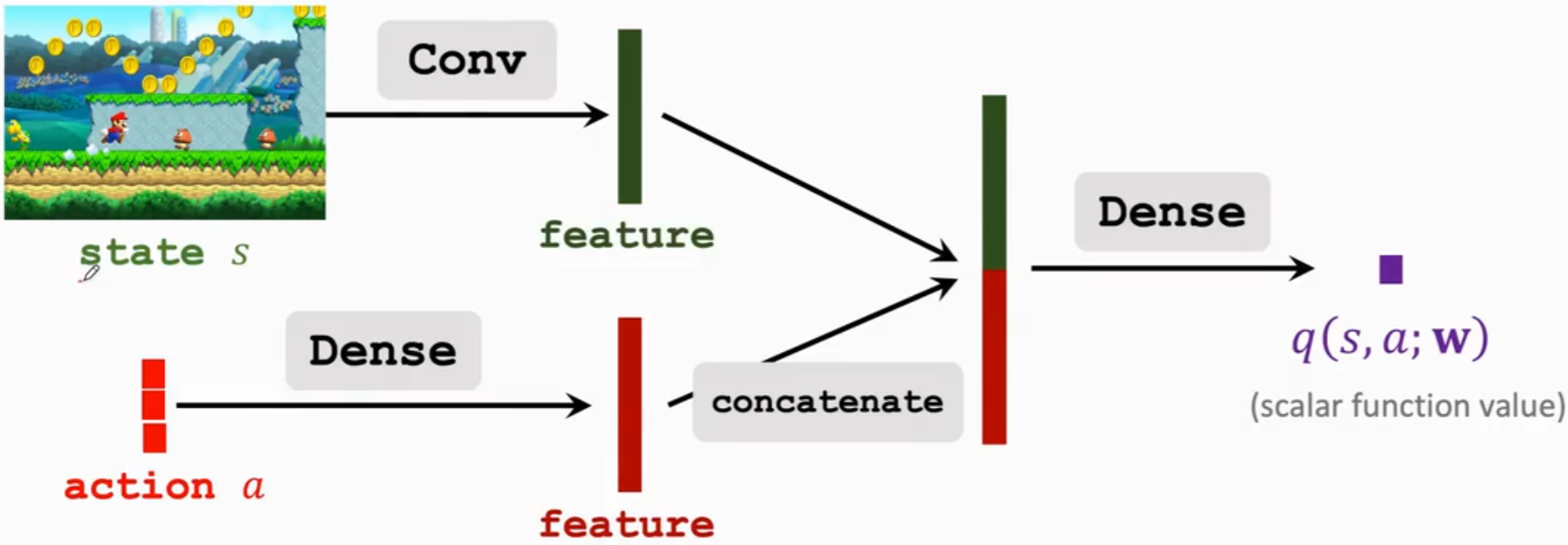
我们使用神经网络 $Q(s,a;w)$ 来近似 $Q^*(s,a)$，其中 w 是要近似的参数，s 是输入，a 是输出是对所有动作的打分。

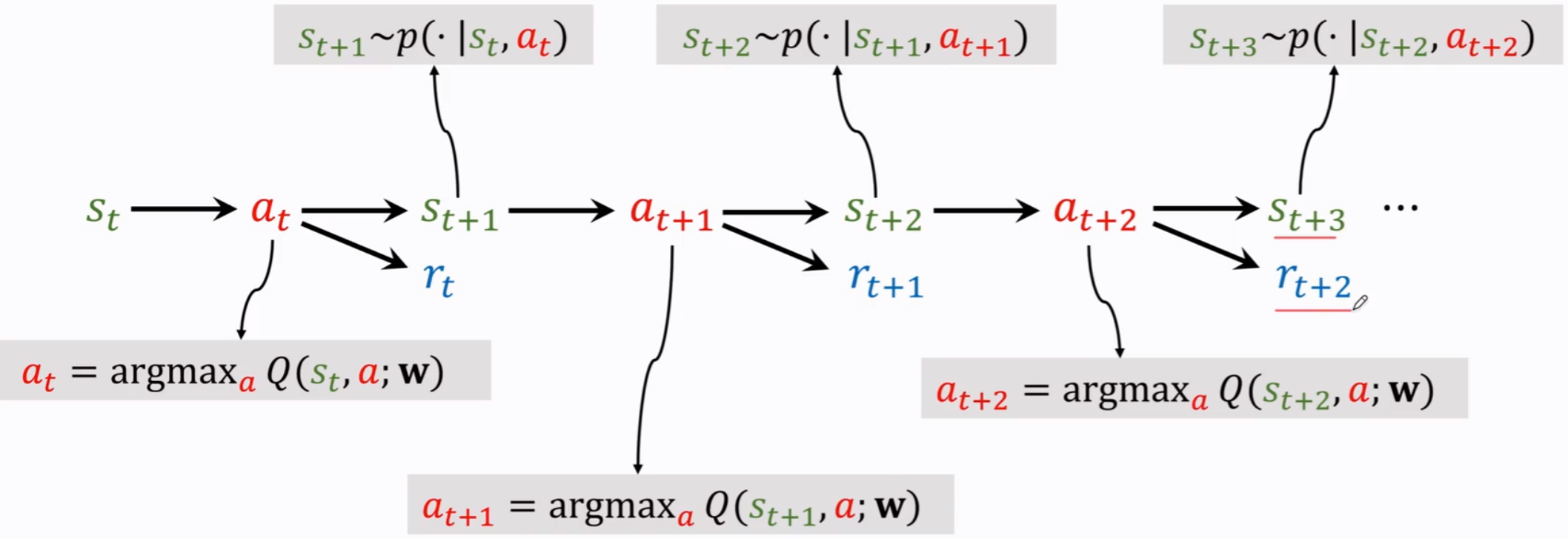
当前观测到状态 $s_t$，用DQN把 $s_t$ 作为输入，为所有动作打分，选出分数最高的动作作为 $a_t$。

agent 作出动作 $a_t$ 后，环境会改变，用状态转移函数 $p$ 随机抽取一个新的状态 $s_{t+1}$，环境还会告诉我们一个回报 $r_t$，这个 $r_t$ 就是训练DQN的关键。

（2）如何训练 DQN

常规的网络训练过程如下：

首先对任务结果做一个预测 $q=Q(w)$
完成任务后获得目标 $y$
计算损失 $L=\frac{1}{2}(q-y)^2$
计算梯度 $\frac{\partial L}{\partial w}=\frac{\partial L}{\partial q}\cdot \frac{\partial q}{\partial w}$
更新参数 $w_{t+1}=w_t-\alpha \cdot\frac{\partial L}{\partial w}|_{w=w_t}$

但这种方式需要完整完成一次任务后才能更新参数，而能否执行一部分任务后就开始更新参数，因此有了 Temporal Difference Learning （TD算法），过程如下：

首先对任务结果做一个预测 $q=Q(w)$
执行一部分任务后，对任务结果再进行预测 $y$，此时的 $y$ 包括已经完成的部分和对剩下部分的预测，因此比 $q$ 更可靠
计算损失 $L=\frac{1}{2}(q-y)^2$
计算梯度 $\frac{\partial L}{\partial w}=\frac{\partial L}{\partial q}\cdot \frac{\partial q}{\partial w}$
更新参数 $w_{t+1}=w_t-\alpha \cdot\frac{\partial L}{\partial w}|_{w=w_t}$

在深度强化学习中，也就是下面这个公式

$$Q(s_t,a_t;w)\approx r_t+\gamma\cdot Q(s_{t+1},a_{t+1};w)$$

对未来奖励总和的期望，就是真实已经观测到的奖励，加在t+1时刻对未来奖励的期望。

首先进行预测 $Q(s_t,a_t;w_t)$
获得TD目标 $y_t=r_t+\gamma\cdot Q(s_{t+1},a_{t+1};w_t)=r_t+\gamma\cdot max_a Q(s_{t+1},a;w_t)$
计算损失 $L_t=\frac{1}{2}[Q(s_t,a_t;w)-y_t]^2$
进行剃度下降 $w_{t+q}=w_t-\alpha\cdot\frac{\partial L_t}{\partial w}|_{w=w_t}$

（3）经验回放

之前我们使用在线梯度下降来更新 $w$，以此来减小TD errer $\delta_t=q_t-t_t$。

我们定义一个经验transition为$(s_t,a_t,r_t,s_{t+1})$，传统的方法再每使用一个transition后就会丢弃它，这回造成经验的浪费。此外传统的方法还忽略了不同经验之间的相关性。

将最近的n个transition存储进一个replay buffer，当有新的经验进来后，就删除老的transition。

每次从buffer中随机抽取一个transition
计算TD error
极端梯度
进行随机梯度下降（实际一般使用minibatch SGD，一次取多个transition）

优先经验回放：为了解决数据的不均匀性，可以使用重要性抽样代替平均采样。可以根据TD error抽样，误差越大的，transition被抽样的概率越大。

学习率比例设置：如果一个transition有较大的抽样概率，那么其学习率应该设置的比较小。

更新TD error：如果一个transition没有被用过，那么就设置它的TD error为最大值，在训练DQN的同时，对TD error进行更新。

三、策略学习

策略函数 $\pi(a|s)$是一个概率密度函数，对每一个给定的状态 $s$，策略函数会抽取一个最优的动作 $a$ 作为将要执行的动作。

理想情况下，列出所有的状态和动作，计算所有状态和动作之间的概率即可。

但是实际情况下有无数个状态，不可能记录所有的状态对应的动作，因此需要函数近似。一般使用神经网络进行近似，即policy network $\pi(a|s;\theta)$

状态价值函数$V_\pi(s_t)=E_A[Q_\pi(s_t,A)]$，状态价值函数可以告诉我们当前的局势好不好。在状态已知时，还可以判断策略好不好，策略越好，$V_\pi$ 越大，任务完成成功率越高，$V_\pi$ 可以表示为：

$$V_\pi(s_t)=E_A[Q_\pi(s_t,A)]=\sum_a\pi(a|s_t)\cdot Q_\pi(s_t,a)$$

使用神经网络替换策略函数，因此得到：

$$V_\pi(s_t;\theta)=\sum_a\pi(a|s_t;\theta)\cdot Q_\pi(s_t,a)$$

给定状态 $s$，策略函数函数越好，价值函数越大。因此可以考虑通过改变神经网络参数 $\theta$，让 $V(s;\theta)$ 变大，基于这个思想，可以求期望：

$$J(\theta)=E_s[V(S;\theta)]$$

策略网络越好，$J(\theta)$ 就越大，为了改变 $\theta$，我们使用策略梯度算法。

观测状态 $s$
更新策略 $\theta=\theta+\beta\cdot\frac{\partial V(s;\theta)}{\partial \theta}$，做梯度上升，因为我们希望价值函数越大越好。

对于离散的动作，使用$\frac{\partial V(s;\theta)}{\partial \theta}=\sum_a \frac{\partial \pi(a|s;\theta)}{\partial \theta}\cdot Q_\pi(s,a)$

对于连续的动作，使用$\frac{\partial V(s;\theta)}{\partial \theta}=E_{A~\pi(\cdot|s;\theta)} [\frac{\partial \pi(a|s;\theta)}{\partial \theta}\cdot Q_\pi(s,a)]$

四、Actor-Crictic

状态价值函数的定义如下：

$$V_\pi(s_t)=\sum_a\pi(a|s_t)\cdot Q_\pi(s_t,a)$$

策略网络（产生动作）：

使用神经网络 $\pi(a|s;\theta)$ 来近似策略函数 $\pi(a|s)$
其中 $\theta$ 是训练的参数

价值网络（产生评判标准）：

使用神经网络 $q(s,a;w)$ 来近似价值函数 $Q_\pi(s,a)$
其中 $w$ 是训练的参数

因此状态价值函数可以写成

$$V_\pi(s_t)=\sum_a\pi(a|s_t;\theta)\cdot Q_\pi(s_t,a;w)$$

同时训练策略网络和价值网络，就称为 Actor-Critic Method，大致步骤如下：

观测当前状态 $s_t$
根据策略函数 $\pi(\cdot|s_t;\theta_t)$ 随机采样获得动作 $a_t$
执行动作 $a_t$，并观测新的状态 $s_{t+1}$ 和回报 $r_t$
更新价值网络的参数 $w$，使用TD算法
更新策略网络的参数 $\theta$，使用策略梯度算法

训练过程中需要同时训练策略网络和价值网络，利用价值网络对策略网络进行评分。训练完成后就不需要价值网络了，只需要策略网络生成动作。

五、蒙特卡洛树搜索（Monte Carlo Tree Search）

5.1 基本思想

蒙特卡洛树搜索的思想是人们必须要向前看很多步，看到未来时间内所有可能的情况，挑选最优的执行动作。

如果我在此时选择执行动作 $a_t$
那么未来一段时间环境的反馈是怎么变化的 $s_{t+1}$
基于这种环境变化，我又会执行动作 $a_{t+1}$
此时环境又会如何变化

如果一个agent能够穷举所有的可能性直到任务完成，那么这个任务一定有很高的成功率。

5.2 过程

（1）选择

根据分数选择一个动作（假想的动作，实际上并不会执行）；

首先对所有可能的动作 $a$，计算得分：

$$score(a)=Q(a)+\eta\cdot\frac{\pi(a|s_t;\theta)}{1+N(a)}$$

其中 $Q(a)$ 是蒙特卡洛树搜索计算的动作价值
$\pi(a|s_t;\theta)$ 是学习好的策略网络，动作越好，策略分数越高
$N(a)$ 是给定环境状态 $s_t$ 情况下，目前为止选择动作 $a$ 的次数，如果同一个动作被探索太多次，该项分母就会变大。

（2）扩展

假想环境更新；

（3）评估

评价状态价值得分 $v$ 和回报 $r$，将动作的分数设为 $\frac{v+r}{22}$；

（4）备份

用动作的分数 $\frac{v+r}{2}$ 更新动作价值：

$$Q(a_t)=mean(the recorded V’s)$$

将以后所有步的状态价值进行平均。

六、连续控制

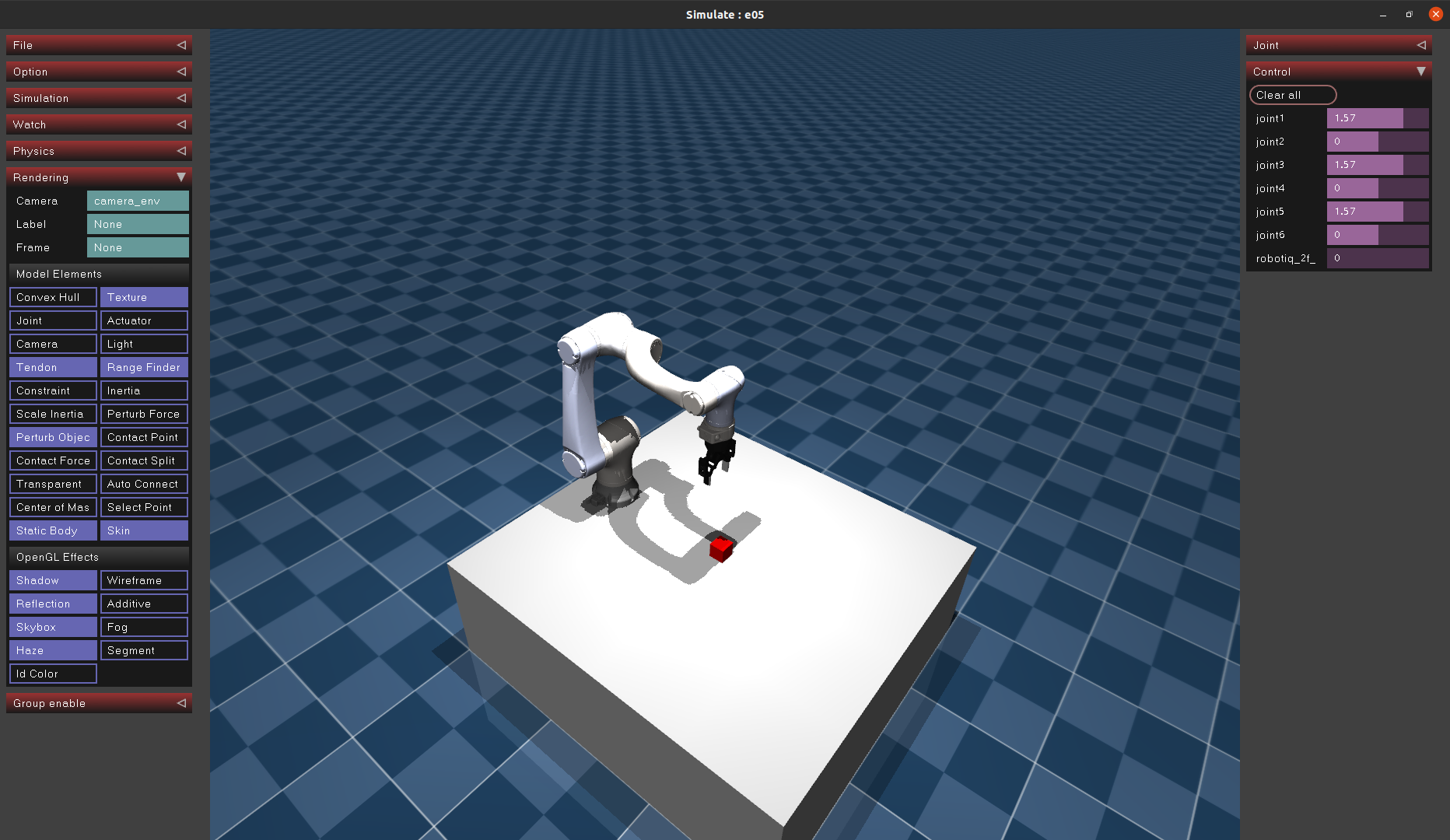
在实际进行强化学习时，可能有离散动作空间（例如上下左右控制游戏人物），也可能是连续动作（机械臂关节控制）。

在进行离散控制时，可以直接使用分类的思想，得到一个onehot向量，每个向量元素代表执行该动作的得分，以此来获得应该执行那种动作。而连续控制中动作空间是有无穷维的，因此不能直接使用这种思想实现连续控制。

比较常规的一种解决思路是将动作空间离散化，但这种方式也有问题，例如机械臂的6个自由度，就算每个自由度离散为360个点，那么整个动作空间也有 $360^6$ 个点，这会造成维度灾难，在训练时非常困难。

因此有两种方式实现连续控制：

确定性策略网络
随机策略网络

6.1 确定策略梯度（Deterministic Policy Gradient DPG）

考虑一个只有2自由度的机械臂，基座运动范围为(0,180)，机械臂运动范围为(0,360)，因此机械臂的动作空间是 $A=[0,180]\times[0,360]$ 的连续集合，动作就是一个二维向量。

DPG 是一种 Actor-Critic 方法

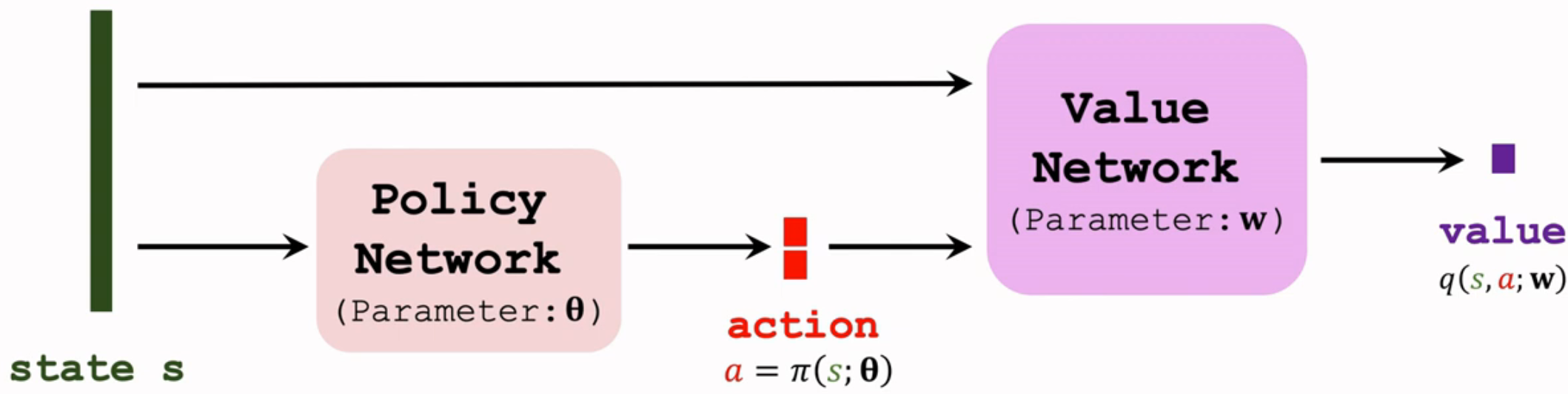
有一个策略网络，控制 agent 运动，它根据状态 s 做出决策 a；
使用策略网络 $a=\pi(s;\theta)$ 根据输入状态 s，输出一个确定的动作 a，这里的动作 a 就是机器人的二维动作向量。
有一个价值网络，不控制 agent，它根据状态 s，给动作 a 打分，从而指导策略网络做出改进。
使用价值网络 $q(s,a;w)$，输入状态 s 和动作 a，输出一个实数 value 是对动作的评价，动作越好，value 越大。

因此 DPG 的原理就是训练这两个网络。

（1）价值网络训练

每次得到一个训练数据 transition $(s_t,a_t,r_t,s_{t+1})$
用价值网络预测当前时刻 t 下的动作价值 $q_t=q(s_t,a_t;w)$
用价值网络预测下一时刻 t+1 的动作价值 $q_{t+1}=q(s_{t+1},a_{t+1}‘;w)$ ，其中 $a_{t+1}’=\pi(s_{t+1};\theta)$，这个动作并不是 agent 真正执行的动作，$a_{t+1}'$ 只用于更新价值网络。
计算 TD error：$\delta_t=q_t-(r_t+\gamma\cdot q_{t+1})$，其中第二项是 TD Target，它一部分是真实观测到的奖励，另一部分是价值网络自己做出的预测。因为我们认为第二项中由于包含本步真实奖励，比单纯的 $q_t$ 更接近真实情况，因此要让 $q_t$ 与 TD Target 接近，也就是让 TD error 尽可能小。
进行梯度下降更新 w：$w=w-\alpha\cdot\gamma_t\cdot\frac{\partial q(s_t,a_t;w)}{\partial w}$

但这其中有一个问题，就是计算 TD error $\delta_t=q_t-(r_t+\gamma\cdot q_{t+1})$ 这一步时，会出现 bootstrapping 问题，也就是如果初始值高估或者低估，那么 TD target 就会有高估或低估，并传播回价值网络自身，导致高估或低估一直存在，解决方案就是用不同的神经网络计算 TD Target，也就是用 Target Networks。

每次得到一个训练数据 transition $(s_t,a_t,r_t,s_{t+1})$
用价值网络预测当前时刻 t 下的动作价值 $q_t=q(s_t,a_t;w)$
用价值网络预测下一时刻 t+1 的动作价值 $q_{t+1}=q(s_{t+1},a_{t+1}‘;w^-)$ ，其中 $a_{t+1}’=\pi(s_{t+1};\theta^-)$
$\pi(s_{t+1};\theta^-)$ 是 Target policy network 用来代替策略网络，它的网络结构和策略网络一模一样，但是参数不一样。
$q(s_{t+1},a_{t+1}';w^-)$ 是 Target value network，它与价值网络结构一样，参数不同。

（2）策略网络训练

训练策略网络，需要靠价值网络评价动作的好坏，从而指导策略网络进行改进。

也就是更新策略网络的参数 $\theta$ 让价值网络认为动作 $a=\pi(s;\theta)$ 更好，也就是改进 $\theta$ 让价值 $q(s,a;w)=q(s,\pi(s;\theta);w)$ 尽可能大。

由于给定状态 s，策略网络会输出一个确定的动作 a，而如果价值网络也是确定的，那么输出的价值就是确定的。

因此问题中只需要改变 $\theta$，使得价值 q 变大，也就是计算 $q(s,a;w)$ 对 $\theta$ 的梯度，然后用梯度上升更新 $\theta$，就可以让 $q$ 变大，这个梯度就叫确定策略梯度 DPG。

$$
g=\frac{\partial q(s,\pi(s;\theta);w)}{\partial\theta}=\frac{\partial a}{\partial \theta}\cdot\frac{\partial q(s,a;w)}{\partial a}
$$

其中 $a=\pi(s;\theta)$，然后进行梯度上升 $\theta=\theta+\beta\cdot g$

策略网络和价值网络联合具体步骤如下：

策略网络做一个决策：$a=\pi(s;\theta)$
计算价值网络的输出：$q_t=q(s,a;w)$
用 DPG 更新策略网络： $\theta=\theta+\beta\cdot \frac{\partial a}{\partial \theta}\cdot\frac{\partial q(s,a;w)}{\partial a}$
利用 Target networks $\pi(s;\theta^-)$ 和 $q(s,a;w^-)$ 计算 $q_{t+1}$
计算 TD error：$\delta_t=q_t-(r_t+\gamma\cdot q_{t+1})$
更新价值网络：$w=w-\alpha\cdot\gamma_t\cdot\frac{\partial q(s_t,a_t;w)}{\partial w}$
更新 Target networks 的参数：$w^-=\tau\cdot w+(1-\tau)\cdot w^-$，$\theta^-=\tau\cdot \theta+(1-\tau)\cdot \theta^-$，其中 $\tau$ 是超参数

6.2 随机策略用于连续控制

首先考虑自由度等于 1 的随机策略连续控制，也就是动作都是实数。

设 $\mu$ 代表均值，和 $\sigma$ 代表标准差，都是状态 s 的函数。

用正态分布的概率密度函数作为策略函数：

$$
\pi(a|s)=\frac{1}{\sqrt{6.28}\sigma}\cdot exp(-\frac{(a-\mu)^2}{2\sigma^2})
$$

对于 d 维情况一样，动作是 d 维向量。

设向量 $\mu$ 代表均值，和向量 $\sigma$ 代表标准差，都是状态 s 的函数。

使用特殊正态分布作为策略函数：

$$
\pi(a|s)=\prod_{i=1}^d\frac{1}{\sqrt{6.28}\sigma_i}\cdot exp(-\frac{(a_i-\mu_i)^2}{2\sigma^2_i})
$$

但这里我们不知道 $\mu$ 和 $\sigma$，也就不知道策略函数。

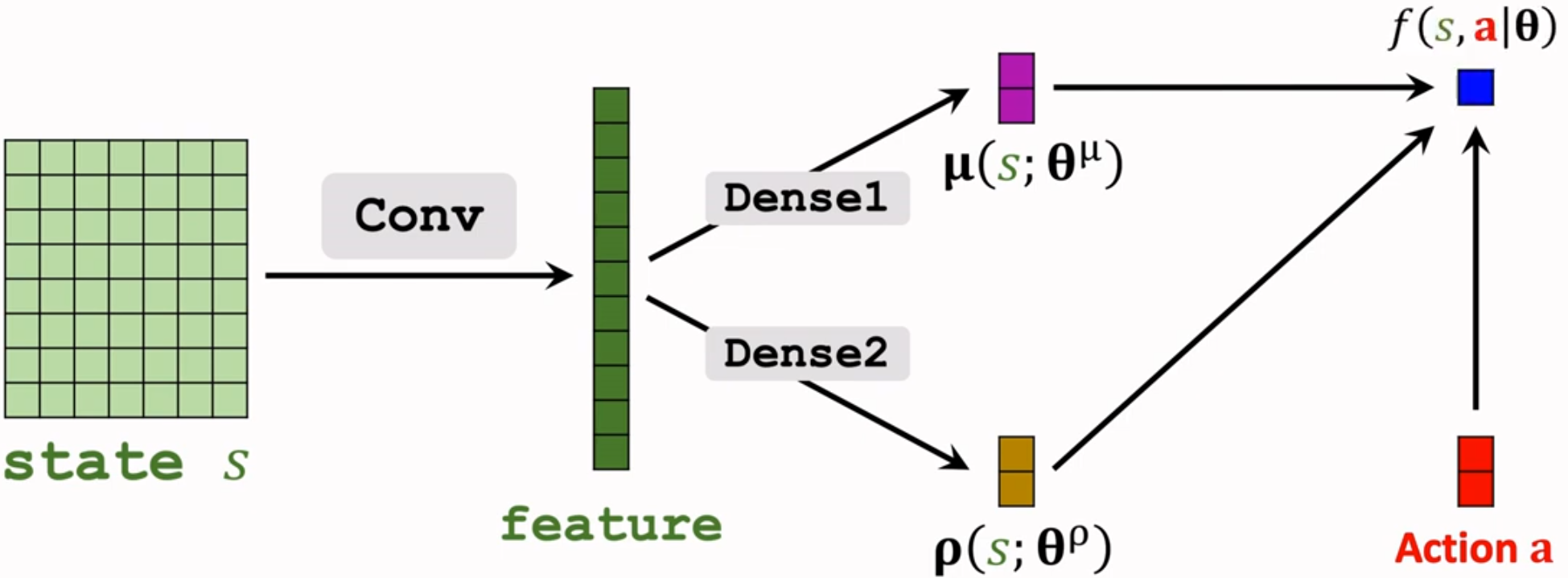
因此可以用神经网络来近似 $\mu(s;\theta^{\mu})$ 和 $\rho(s;\theta{\rho})$，其中 $\rho_i=ln\sigma_i^2$

将策略函数进行取对数，将连乘变成连加，得到辅助神经网络 $f(s,a;\theta)=\sum^d_{i=1}[-\frac{\rho_i}{2}-\frac{(a_i-\mu_i)^2}{2\cdot exp(\rho_i)}]$，计算 f 关于其中卷积层和全连接层的参数的梯度，进而实现反向传播更新参数。

参考：

王树森. 强化学习课程(Youtube)