【强化学习算法】近端优化策略PPO

基础知识

Value-Based

包括 Q-Learning，DQN等方法。

（1）Q值与V值

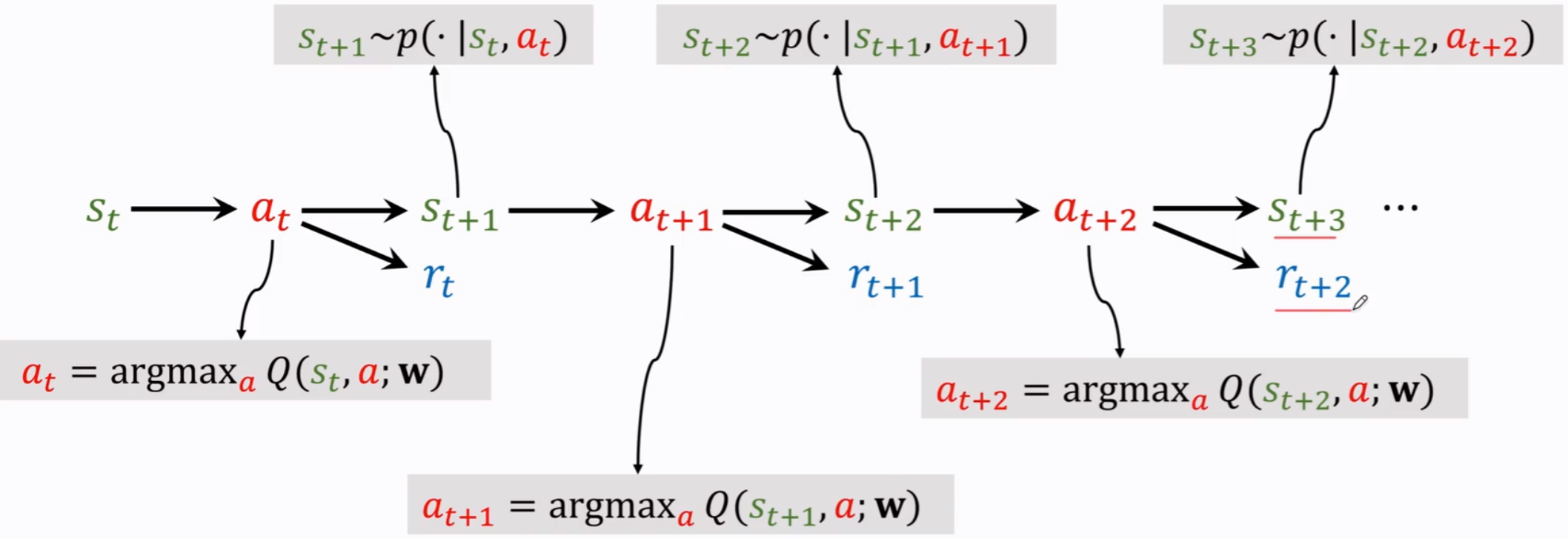
V值：当前状态下，未来所有状态奖励的总和。（当前状态复制N份，每个状态根据策略选择不同的可能的行为，一直到最终状态，计算N个奖励的平均值）
计算的是当前策略选择动作的合理性
Q值：衡量动作节点的价值。（当前动作复制N份，每个动作一直与环境交互记录所获得的奖励，计算N个奖励的平均值）
Q值与策略没有直接相关，而与环境的状态转移概率相关。

（2）蒙特卡洛

对于某一个状态，先根据当前状态走到头（策略可能生成不同的动作，分成不同的分支），计算所有的奖励 r，然后回溯计算G值。

G值：$G=r+\gamma \cdot G$，G值代表某个状态到最终状态的奖励总和
V值就是状态S的N个复制的G值的平均值。（和策略紧密相关，策略不同，N个状态S得到的动作A的概率不同）

**缺点在于每次都需要所有的状态都从头走到尾，可能需要较长时间才能更新G值。**因此考虑使用估算的方法：

$$
V(S_t)=V(S_t)+\alpha[G_t-V(S_t)]
$$

也就是前一时刻估计的V值，利用超参数学习率，使V值向 $G_t$ 值接近，这样只要任意一个状态走完返回G值，就可以更新一次。

但这种方式仍然需要分支走到最终状态才能进行更新。因此发明了时序查分（Temporal Difference，TD）算法

与蒙特卡洛不同，TD算法只需要走N步，就可以开始回溯更新。即假设N步之后就达到了最终状态。如果最终状态没有任何一个分支走过，则设状态为0，如果有分支走过这个状态，那么这个状态的V值就是当前值。

$$
V(S_t)=V(S_t)+\alpha[R_{t+1}+\gamma V(S_{t+1})-V(S_t)]
$$

其中 $R_{t+1}+\gamma V(S_{t+1})$ 就相当于蒙特卡洛计算的 $G_t$ 值，$V(S_{t+1})$ 代表N步之后的状态V值。

Policy-Based

（1）策略梯度

策略梯度PG的思想就是直接计算神经网络，输入state输出action，这个过程不计算Q。

PG的目的是最大化整个 episode 回合的 total reward，由于 actor 和 environment 都存在随机性，因此 $R_\theta=\sum^T_{t=1}r_t$ 是随机的，所以要最大化它的期望 $\bar{R_\theta}$ 来衡量 actor 的好坏。

$$
\bar{R_\theta}=\sum_\tau R(\tau)P(\tau|\theta)\approx\frac{1}{N}\sum^N_{n=1}R(\tau^n)
$$

其中 $P(\tau|\theta)$ 是策略选择动作得到轨迹 $\tau$ 的概率，对所有轨迹 $\tau$ 得到的奖励求平均就是 $\bar{R_\theta}$

$$
\theta^*=\mathop{\arg\max}\limits_{\theta}\bar{R_\theta}
$$

PG算法就是优化网络 $\theta$ 使奖励期望最大，也就是利用梯度下降策略使 $\bar{R_\theta}$ 对 $\theta$ 求导梯度下降来优化网络。

$$
\nabla\bar{R_\theta}=\sum_\tau R(\tau)\nabla P(\tau|\theta)=\sum_\tau R(\tau)P(\tau|\theta)\frac{\nabla P(\tau|\theta)}{P(\tau|\theta)}
$$
利用 log 函数的导数形式，写成：
$$
=\sum_\tau R(\tau)P(\tau|\theta)\nabla logP(\tau|\theta)\approx\frac{1}{N}\sum^N_{n=1}R(\tau^n)\nabla logP(\tau^n|\theta)
$$
其中 $P(\tau|\theta)=p(s_1)\prod^T_{t=1}p(a_t|s_t,\theta)p(r_t,s_{t+1}|s_t,a_t)$，也就是表示从 $s_t$ 到 $a_t$ 以及从 $a_t$ 到 $s_{t+1}$ 的概率，连乘代表当前轨迹出现的概率。

又因为 log 会将连乘转换为连加，也就是

$$
logP(\tau|\theta)=logp(s_1)+\sum^T_{t=1}[logp(a_t|s_t,\theta)+logp(r_t,s_{t+1}|s_t,a_t)]
$$
因此其对 $\theta$ 求导为：

$$
\nabla logP(\tau|\theta)=\sum^T_{t=1}\nabla logp(a_t|s_t,\theta)
$$
故

$$
\nabla \bar {R_\theta}\approx\frac{1}{N}\sum^N_{n=1}R(\tau^n)\nabla logP(\tau^n|\theta)=\frac{1}{N}\sum^N_{n=1}R(\tau^n)\sum^T_{t=1}\nabla logp(a_t|s_t,\theta)=\frac{1}{N}\sum^N_{n=1}\sum^T_{t=1}R(\tau^n)\nabla logp(a_t|s_t,\theta)
$$

也就是在 t 回合的 state 下，采取的 action ，如果得到的 total reward 是正的，就希望更新模型使得几率 $p(a^n_t|s^n_t,\theta)$ 越大越好，反之亦然。